Problem#1
In Fig. 1a, two circular loops, with different currents but the same radius of 4.0 cm, are centered on a y axis. They are initially separated by distance L = 3.0 cm, with loop 2 positioned at the origin of the axis.The currents in the two loops produce a net magnetic field at the origin, with y component By..That component is to be measured as loop 2 is gradually moved in the positive direction of the y axis. Figure 1b gives By as a function of the position y of loop 2. The curve approaches an asymptote of By = 7.20 μT as y : → ∞. The horizontal scale is set by ys = 10.0 cm. What are (a) current i1 in loop 1 and (b) current i2 in loop 2?
 |
| Fig.1 |
Answer:
Because By can be zero, the current direction on the two coils is different so that the direction of the magnetic field is different.
The magnitude field a distance y along the central axis from coil is given by:
B (y) = μ0iR2/{2(R2 + y2)3/2}
 |
| Fig.2 |
For coil 1: At the center of loop y = L
B1 = μ0i1R2/{2(R2 + L2)3/2} (towards the positive y axis)
For coil 2: At the center of loop y
B2(y) = μ0i2R2/{2(R2 + y2)3/2} (towards the negative y axis)
At point O from each coil, the magnetic field from each coil point in the +y direction
By,net = B1 + B2
By,net = μ0i1R2/{2(R2 + L2)3/2} ─ μ0i2R2/{2(R2 + y2)3/2}
(a) The curve approaches an asymptote of By = 7.20 μT as y : → ∞,
By,net = μ0i1R2/{2(R2 + L2)3/2}
7.20 x 10─6 T = (4π x 10─7 Tm/A)(i1)(0.04 m)2/{2[(0.04 m)2 + (0.03 m)2]3/2}
7.20 x 10─6 = (4π x 10─7)(6.4)i1
i1 = 0.895 A
(b) from the graph it is shown that for y = 6.0 cm the total magnetic field is By,net = 0, then
0 = μ0i1R2/{2(R2 + L2)3/2} ─ μ0i2R2/{2(R2 + y2)3/2}
i1/(R2 + L2)3/2 = i2/(R2 + y2)
i1/i2 = [(R2 + L2)/(R2 + y2)]3/2
0.895 A/i2 = {[(0.04 m)2 + (0.03 m)2]/[(0.04 m)2 + (0.06 m)2]}3/2
0.895 A/i2 = (25/52)3/2
0.895 A/i2 = 0.3333
i2 = 2.68 A
Problem#2
A circular loop of radius 12 cm carries a current of 15 A. A flat coil of radius 0.82 cm, having 50 turns and a current of 1.3 A, is concentric with the loop.The plane of the loop is perpendicular to the plane of the coil. Assume the loop’s magnetic field is uniform across the coil. What is the magnitude of (a) the magnetic field produced by the loop at its center and (b) the torque on the coil due to the loop?
Answer:
(a) Assume we have loop concentric with a coil, the plane of the coil is perpendicular to the plane of the loop as shown in figure, the magnetic field due to the loop at the center of the loop is given by:
B = μ0i/2R
B = (4π x 10─7 Tm/A)(15 A)/(2 x 0.12 m) = 7.9 x 10─5 T
(b) the torque magnitude excreting on the coil due to the magnitude field of the loop is given by:
τ = μ x B
τ = μB sin θ
 |
| Fig.3 |
where μ is the magnetic dipole moment of the coil and θ is the angle between the magnetic dipole moment and the magnetic field, as shown in the figure μ B, the magnetic dipole moment is given by:
μ = NiA
where N is the number of turns in the coil and A = πR2 is the area of the coil, hence:
μ = πNiR2
so that
τ = μB sin θ = πNiR2B
τ = π x 50 x 1.3 A x (0.82 x 10─2 m)2 x (7.9 x 10─5 T)
τ = 1.1 x 10─6 N.m
Problem#3
In Fig. 4, current i = 56.2 mA is set up in a loop having two radial lengths and two semicircles of radii a = 5.72 cm and b = 9.36 cm with a common center P. What are the (a) magnitude and (b) direction (into or out of the page) of the magnetic field at P and the (c) magnitude and (d) direction of the loop’s magnetic dipole moment?
 |
| Fig.4 |
(a) Magnetic field, B = 0 from straight segments at P.
Magnetic field at center of circular arc given by
B = μ0iφ/4πR
(a) The magnitude of the magnetic field at P is
Bnet = μ0iπ/4πb + μ0iπ/4πa
Bnet = (μ0i/4)(1/b + 1/a)
= [(4π x 10─7 Tm/A)(56.2 x 10─3 A)/4](1/0.0936 m + 1/0.0572 m)
Bnet = 4.97 x 10─7 T
(b) Using the right hand rule, the B direction points into the page.
(c) magnitude direction of the loop’s magnetic dipole moment is
μ = NIA
μ = ½πI(a2 + b2)
= ½π x )(56.2 x 10─3 A)[(0.0572 m)2 + (0.0936 m)2]
μ = 1.06 x 10─3 A.m2
(d) direction of the loop’s magnetic dipole moment is into the page (the same direction as n)
Problem#4
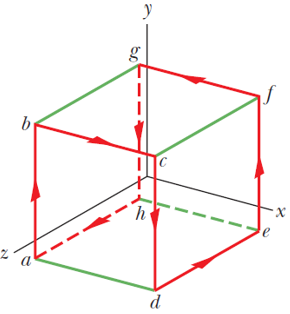
In Fig. 4, a conductor carries 6.0 A along the closed path abcdefgha running along 8 of the 12 edges of a cube of edge length 10 cm. (a) Taking the path to be a combination of three square current loops (bcfgb, abgha, and cdefc), find the net magnetic moment of the path in unit vector notation. (b) What is the magnitude of the net magnetic field at the xyz coordinates of (0, 5.0 m, 0)?
 |
| Fig.5 |
Answer:
(a) The magnitude of the magnetic dipole moment is given by
μ = iAn
μ = I x Abcfgbj + I x Aabgha (─i) + I x Acdefc i
μ = I x Abcfgbj
μ = 6.0 A x (0.10 m)2j = (0.060 A.m2)j
 |
| Fig.6 |
(b) The magnetic field produced by a current-carrying coil, which is a magnetic dipole, at a point P located a distance z along the coil’s perpendicular central axis is parallel to the axis and is given by
B(z) = μ0μ/(2πz3)
Then, the magnitude of the net magnetic field at the xyz coordinates of (0, 5.0 m, 0) is
B(y) = μ0μ/(2πy3)
B(y) = (4π x 10─7 T.m/A)(0.060 A.m2)j/[2π x (5.0 m)3]
B = (9.60 x 10─11 T)j = (96 pT)j
Post a Comment for "A Current-Carrying Coil as a Magnetic Dipole Problems and Solutions 2"