Ampere’s Law Problems and Solutions 2

 Problem#1

The current density inside a long, solid, cylindrical wire of radius a = 3.1 mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J = J₀r/a, where J₀ = 310 A/m². Find the magnitude of the magnetic field at (a) r = 0, (b) r = a/2, and (c) r = a.

Answer:
Apply Ampere’s law to a circle of radius r inside the wire:

∮B. ds  = μ₀i_enc

so the magnetic field at r ≤ a is

∮B. ds  = 2πrB = μ₀i_enc = μ₀ ∫JdA
2πrB = μ₀∫₀^r J₀(r/a) 2πr dr = μ₀J₀r²/3a
B(r) = μ₀J₀r²/3a

(a) at r = 0, B = 0

(b) at r = a/2, we have

B(r) = μ₀J₀r²/3a
B(r = a/2) = (4π x 10^─7 Tm/A)(310 A/m²)(3.1 x 10^─3 m/2)²/(3 x 3.1 x 10^─3 m) = 1.0 x 10^─7 T

(c) at r = a
B(r = a) = μ₀J₀r²/3a = μ₀J₀a/3
B(r = a) = (4π x 10^─7 Tm/A)(310 A/m²)(3.1 x 10^─3 m)/3 = 4.0 x 10^─7 T

Problem#2
In Fig. 1, a long circular pipe with outside radius R = 2.6 cm carries a (uniformly distributed) current i = 8.00 mA into the page. A wire runs parallel to the pipe at a distance of 3.00R from center to center. Find the (a) magnitude and (b) direction (into or out of the page) of the current in the wire such that the net magnetic field at point P has the same magnitude as the net magnetic field at the center of the pipe but is in the opposite direction.

Fig.1

Answer:
Want B at P and B at P₁ to have the same magnitude but opposite directions.

The pipe will not contribute to B at P₁ because ∮B. ds  = μ₀i_enc = μ₀ x 0 = 0

B due to the pipe at P is gotten by taking an Amperian loop (circle) centered on the pipe

∮B. ds  = μ₀i_net
B(2πr) = μ₀I
B = μ₀I/(2π x 2R)
B = μ₀I/4πR (up)

Fig.2

Only true because set as a condition in the problem

B_P1 (wire) =  B_P (pipe) ─ B_P (wire)
μ₀I_w/(2π x 3R) = μ₀I_P/4πR ─ μ₀I_w/2πR
I_w/3 = I_P/2 ─ I_w
I_w = 3I_P/8 = 3 x 8.00 mA/8 = 3.00 mA

Problem#8
Figure 3 shows a cross section of a long conducting coaxial cable and gives its radius (a, b, c). Equal but opposite currents i are uniformly distributed in the two conductors. Derive expressions for B(r) with radial distance r in the ranges (a) r < c, (b) c < r < b, (c) b < r < a, and (d) r > a. (e) Test these expressions for all the special cases that occur to you. (f) Assume that a = 2.0 cm, b = 1.8 cm, c = 0.40 cm, and i = 120 A and plot the function B(r) over the range 0 < r < 3 cm.

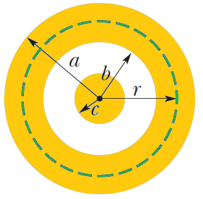Fig.3

Answer:
Due to the symmetry, we can easily solve this problem using Ampere's Law

∮B. ds  = μ₀i_enc

where i_enc is the current that passes through the two-dimensional area enclosed by the contour. From the Biot-Savart Law we know the magnetic field forms concentric loops around the wire, and due to the symmetry we know that the field at all points on the loop must have the same magnitude. We choose the contour to be concentric loops around the wire, and then the integral is

∮B. ds  = B(2πr) = μ₀i_enc

where r is the distance from the center of the wire

(a) the magnetic field at r < c is

B(2πr)  = μ₀i_enc

For r < c, not all of the current is enclosed by the contour. We need to determine the current density J, which is the current per unit area, J = I/A. Then the current enclosed is J times the area enclosed. For r < c, J_c = I/πc² and

J_C = J_r
I/(πc²) = i_enc/(πr²)
i_enc = Ir²/c²

so that
B(2πr)  = μ₀(Ir²/c²)

B(r) = μ₀Ir/2πc² (linear function)

(b) the magnetic field at c < r < b is

B(2πr)  = μ₀i_enc

all of the inner current is enclosed and none of the outer current, so the field in this region is just

B(2πr)  = μ₀I
B(r) = μ₀I/2πr (hyperbolic)

(c) for b < r < a is part of the outer current (which is in the opposite direction) is enclosed, so we have to determine the current density J in this case. The full current is still I, but now the area is πa² – πb², giving a current density of

J_c = I/[π(a² ─ b²)]

The magnetic field is now given by

B(2πr) = μ₀i_enc

With
i_enc = I ─ Jπ(r² ─ b²)
i_enc = I ─ I[(πr² ─ πb²)/(πa² ─ πb²)]
i_enc = I{1 ─ [(r² ─ b²)/(a² ─ b²)]}
i_enc = I{(a² ─ r²)/(a² ─ b²)}

therefore:
B(r)  = (μ₀I/2πr){(a² ─ r²)/(a² ─ b²)} with the direction still counterclockwise loops.

(d) For r > a, all of the outer current (which is in the opposite direction as the inner current) is enclosed, so the net current is zero and B = 0.

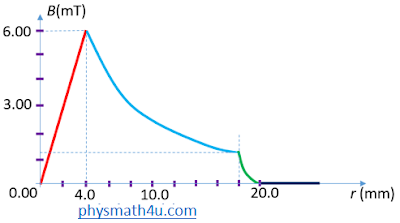
(e) See sketch below. Note that for r < c the field is increasing linearly. For c < r < b, the field falls as 1/r. In the region b < r < a, the field falls off more quickly than 1/r and for r > a the field is zero (B = 0).

Fig.4

(f) Assume that a = 2.0 cm, b = 1.8 cm, c = 0.40 cm, and i = 120 A and plot the function B(r) over the range 0 < r < 3 cm.

For r < c:
B(r = c) = μ₀Ir/2πc² = (4π x 10^─7 Tm/A)(120 A)/[2π x 0.004 m] = 0.0060 T = 6.0 mT

For c < r < b:                                              
B(r = b) = μ₀I/2πr = (4π x 10^─7 Tm/A)(120 A)/[2π x 0.018 m] = 0.00133 T = 1.33 mT

For b < r < a:
B(r = a)  = (μ₀I/2πr){(a² ─ r²)/(a² ─ b²)} = 0

For r > a: B(r > a) = 0

Fig.5