Q#8
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?Answer:
The torque acting on the particle about 50 cm away from the line of motion
= mg(0.50) Nm.
Where m = mass of the particle in kg, g = acceleration due to gravity in m/s² and r = 50 cm = 0.50 m.
This torque cannot produce any angular acceleration in the particle because there is no force in the opposite direction of the weight at 50 cm east of the line of motion. For a torque to be effective through a force, there must be equal and opposite non-linear force acting on the particle.
Q#9
If several forces act on a particle, the torque on the particle may be obtained by first finding the resultant of the force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect a common point?
Answer:
Let F1, F2, F3 .... be the forces acting on the particle and position vector of the particle from the point O (About which torque is being calculated) is r. Then the torque on the particle is equal to,
Γ = r x F1 + r x F2 + r x F3 .
= r x (F1 + F2 + F3 ....) {Because vector cross product is distributive over addition}
= r x F
So, The Torque of the resultant force is equal to the sum of torques of individual forces on a particle.
Hence Proved.
But, if the forces act on different particles of a body such that their lines of actions intersect a common point then also this result is valid. Because we can shift the forces along their lines of action till their ends come to the point of intersection (Equivalent forces). This will not change the torque effect of a force (Since the magnitude of the torque of a force = Magnitude of the force x Shortest distance of the line of action of the force from the point about which torque is being calculated). Having done this we have a condition like first part where all the forces act at a point. So, again
Γ = r x F1 + r x F2 + r x F3 .
= r x (F1 + F2 + F3 ....) {Because vector cross product is distributive over addition}
= r x F
So, The Torque of the resultant force is equal to the sum of torques of individual forces on a body.
Q#10
If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?
Answer:
If the sum of all the forces acting on a body is zero then it is not necessarily in equilibrium. In fact, it will be in translatory equilibrium but may not be in rotational equilibrium. Suppose two equal and opposite forces having their line of actions at a certain distance apart act on a body, then the body will remain stationary at the point but will have rotation due to the torque produced.
If the sum of all the forces acting on a particle is zero then it is necessarily in equilibrium because there will not be a distance between antiparallel forces.
Q#11
If the angular momentum of a body is found to be zero about a point, is it necessary that it will also be zero about a different point?
Answer:
No. We can express the angular momentum of a body about a point as mvr. Since it depends on 'r', it will be different about different points.
Q#12
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
Answer:
Let us understand it with a simple example as in the figure below:
Answer:
We can understand the reason considering the body of the fat person in two parts - Legs up to waist as one part and rest of the body as the second part. (See diagram below).
Γ = r x F1 + r x F2 + r x F3 .
= r x (F1 + F2 + F3 ....) {Because vector cross product is distributive over addition}
= r x F
So, The Torque of the resultant force is equal to the sum of torques of individual forces on a particle.
Hence Proved.
But, if the forces act on different particles of a body such that their lines of actions intersect a common point then also this result is valid. Because we can shift the forces along their lines of action till their ends come to the point of intersection (Equivalent forces). This will not change the torque effect of a force (Since the magnitude of the torque of a force = Magnitude of the force x Shortest distance of the line of action of the force from the point about which torque is being calculated). Having done this we have a condition like first part where all the forces act at a point. So, again
Γ = r x F1 + r x F2 + r x F3 .
= r x (F1 + F2 + F3 ....) {Because vector cross product is distributive over addition}
= r x F
So, The Torque of the resultant force is equal to the sum of torques of individual forces on a body.
Q#10
If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?
Answer:
If the sum of all the forces acting on a body is zero then it is not necessarily in equilibrium. In fact, it will be in translatory equilibrium but may not be in rotational equilibrium. Suppose two equal and opposite forces having their line of actions at a certain distance apart act on a body, then the body will remain stationary at the point but will have rotation due to the torque produced.
If the sum of all the forces acting on a particle is zero then it is necessarily in equilibrium because there will not be a distance between antiparallel forces.
Q#11
If the angular momentum of a body is found to be zero about a point, is it necessary that it will also be zero about a different point?
Answer:
No. We can express the angular momentum of a body about a point as mvr. Since it depends on 'r', it will be different about different points.
Q#12
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
Answer:
Let us understand it with a simple example as in the figure below:
I calculated the net torque measured from point P (I'll skip the designations such as m1, r1, m2 etc. and get to the value):
(1m)2N + (5m)2N – (4m)3N = 0
Now, let's calculate the net torque from Q:
(−2m)2N + (2m)⋅2N – (1m)3N = −3 N
From this it seems, that the body doesn't rotate around an axis in P, but does around the axis in Q.
So, if the resultant torque of all the forces acting on a body is zero about a point, it is not necessary that it will be zero about any other point.
Q#13
A body is in transitional equilibrium under the actions of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
Answer:
Yes. In an inertial or equivalent frame of reference, It will be zero about any other point.
Q#14
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than slightly half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
Answer:
The weight of the projected part produces a torque that will tend to overturn the brick about the edge of the table while the weight of the part on the table produces a torque that will tend to restore the brick from overturning. Assuming a uniform density of the brick, in the first case- the weight of projected part will be less than the weight of the part on the table. Also, the distance of the line of action of the weight of the projected part from the edge of the table is less in comparison to the other part. Hence the overturning torque, in this case, will be less than the restoring torque. So, the brick remains at rest.
The situation is just reverse in the second case where the overturning torque is greater than the restoring torque, so the brick overturns and falls.
Q#15
When a fat person tries to touch his toes keeping the legs straight, he generally falls. Explain with references to figure (10-Q2).
(1m)2N + (5m)2N – (4m)3N = 0
Now, let's calculate the net torque from Q:
(−2m)2N + (2m)⋅2N – (1m)3N = −3 N
From this it seems, that the body doesn't rotate around an axis in P, but does around the axis in Q.
So, if the resultant torque of all the forces acting on a body is zero about a point, it is not necessary that it will be zero about any other point.
Q#13
A body is in transitional equilibrium under the actions of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
Answer:
Yes. In an inertial or equivalent frame of reference, It will be zero about any other point.
Q#14
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than slightly half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
Answer:
The weight of the projected part produces a torque that will tend to overturn the brick about the edge of the table while the weight of the part on the table produces a torque that will tend to restore the brick from overturning. Assuming a uniform density of the brick, in the first case- the weight of projected part will be less than the weight of the part on the table. Also, the distance of the line of action of the weight of the projected part from the edge of the table is less in comparison to the other part. Hence the overturning torque, in this case, will be less than the restoring torque. So, the brick remains at rest.
The situation is just reverse in the second case where the overturning torque is greater than the restoring torque, so the brick overturns and falls.
Q#15
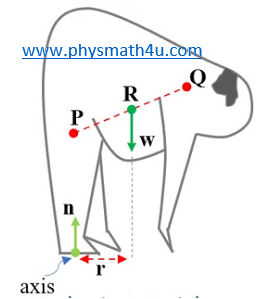
When a fat person tries to touch his toes keeping the legs straight, he generally falls. Explain with references to figure (10-Q2).
Answer:
We can understand the reason considering the body of the fat person in two parts - Legs up to waist as one part and rest of the body as the second part. (See diagram below).
Center of the mass of the first part is at P (Somewhere near the knees) and the center of the mass of the second part is at Q (Somewhere near the chest). So, the center of mass of the whole body is at R on the line PQ. The total weight of the fat person acts at R and the Normal force by the ground on his body (Which is also equal to w) acts opposite to the weight at his toes n. Though both weight and the Normal force are equal and opposite, their lines of action are not the same. Their lines of action are parallel having some distance d between them. So, these antiparallel forces produce a torque equal to rw on the fat person (Which is clockwise in the figure), and he generally falls.



Post a Comment for "Answers to Problems on (Rotational Mechanics) HC Verma's Questions for Short Answer (8-15)"