Q#9
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?Answer:
The potential energy of an object is always with some zero potential energy reference point. If the mean position is chosen as a reference point then the potential energy will never be negative. It may be negative if some other point is selected as zero potential energy reference.
Q#10
The energy of a system in simple harmonic motion is given by E = ½m⍵²A². Which of the two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
Answer:
The formula is for assessing the energy of a particle of mass m in SHM having amplitude A. If the mass is same the particle having larger amplitude will have greater energy. Though both statements are true the amplitude cannot increase itself until some work is done on the particle or some energy is given to it. So, the statement (B) is more appropriate.
Q#11
A pendulum clock gives correct time at the equator. Will it gain time or lose time as it is taken to the poles?
Answer:
At the poles, the value of g is more than the equator. The time period of the pendulum will decrease since T = 2π√(l/g). It means the oscillations will be faster and hence the clock will gain time.
Q#12
Can a pendulum clock be used in an earth satellite?
Answer:
In an earth satellite the net acceleration due to the gravity is zero so the bob of the pendulum will be weightless and it will not oscillate. Thus the pendulum clock cannot be used in an earth satellite.
Q#13
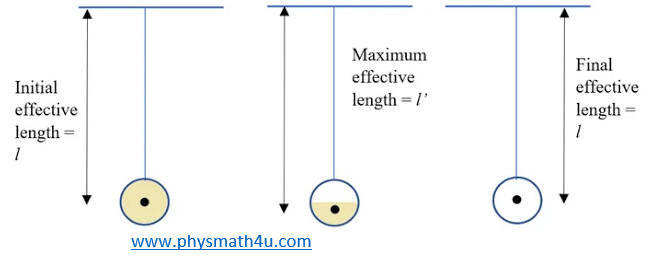
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for the simple pendulum is valid with the distance between the point of suspension and center of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
Answer:
The time period is given as T = 2π√(l/g).
It is clear from this expression that the time period depends only upon the effective length of the pendulum as g is constant at a place.
Initially, the effective length of the pendulum l is the distance between the center of the bob to the point of support. As the water leaks out the center of mass of the water in the bob goes down. So the combined center of mass of the bob also goes down, thus the effective length increases. Thus the time period begins to increase. Though the CoM of the water goes down till the last drop the mass of the water continuously goes reducing till zero. So the combined center of mass after going down to a certain point again begins to go up till it reaches the center of the hollow sphere. Thus the effective length of the pendulum after reaching a maximum slowly reduces back to its original length. The effect is that the time period of the pendulum slowly increases and then reaching a maximum begins to reduce and finally its value becomes the original value.
Q#14
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
Answer:
Yes.
The time period of the vertical oscillation is given by
T = 2π√(m/k)
When the block is in equilibrium,
mg = ks {where s is the extension of the spring}
k = mg/s
Thus T = 2π√(ms/mg) = 2π√(s/g)
Thus the time period of the vertical oscillation can be found out by measuring the extension of the spring when the block is in equilibrium.
Q#15
A platoon of soldiers marches on a road in steps according to the sound of a Marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
Answer:
The march in step is a type of forced oscillation of the bridge. If the frequency of the steps be near to the frequency of the bridge the resonance may occur that will result in a very large amplitude of the bridge oscillation. It will be damaging to the bridge. Hence the march on the bridge is by breaking the steps.
Q#16
The force acting on a particle moving along X-axis is F = -k(x - v₀t) where k is a positive constant. An observer moving at a constant velocity v₀ along the X-axis looks at the particle. What kind of motion does he find for the particle?
Answer:
F = -kx + kv₀t
The force has two part. One is dependent on displacement and the other is dependent on the time. (The first part is negative while the other is positive, the second part is ever-increasing.) So, it is not a simple harmonic motion. The observer is moving with a constant velocity so he still observes from an inertial frame. The observer will also find that it is not a simple harmonic motion.
Q#14
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
Answer:
Yes.
The time period of the vertical oscillation is given by
T = 2π√(m/k)
When the block is in equilibrium,
mg = ks {where s is the extension of the spring}
k = mg/s
Thus T = 2π√(ms/mg) = 2π√(s/g)
Thus the time period of the vertical oscillation can be found out by measuring the extension of the spring when the block is in equilibrium.
Q#15
A platoon of soldiers marches on a road in steps according to the sound of a Marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
Answer:
The march in step is a type of forced oscillation of the bridge. If the frequency of the steps be near to the frequency of the bridge the resonance may occur that will result in a very large amplitude of the bridge oscillation. It will be damaging to the bridge. Hence the march on the bridge is by breaking the steps.
Q#16
The force acting on a particle moving along X-axis is F = -k(x - v₀t) where k is a positive constant. An observer moving at a constant velocity v₀ along the X-axis looks at the particle. What kind of motion does he find for the particle?
Answer:
F = -kx + kv₀t
The force has two part. One is dependent on displacement and the other is dependent on the time. (The first part is negative while the other is positive, the second part is ever-increasing.) So, it is not a simple harmonic motion. The observer is moving with a constant velocity so he still observes from an inertial frame. The observer will also find that it is not a simple harmonic motion.
Post a Comment for "Answers to Problems on (Simple Harmonic Motion) HC Verma's Questions for Short Answer (9-16)"