Problem#1
A student builds and calibrates an accelerometer, which she uses to determine the speed of her car around a certain unbanked highway curve. The accelerometer is a plumb bob with a protractor that she attaches to the roof of her car. A friend riding in the car with her observes that the plumb bob hangs at an angle of 15.0° from the vertical when the car has a speed of 23.0 m/s. (a) What is the centripetal acceleration of the car rounding the curve? (b) What is the radius of the curve? (c) What is the speed of the car if the plumb bob deflection is 9.00° while rounding the same curve?
Answer:
(a) While the car negotiates the curve, the accelerometer is at the angle θ.
∑Fy = may
T cosθ – mg = 0
T cosθ = mg (*)
And
∑Fx = mac
T sinθ = mac (**)
where r is the radius of the curve, and v is the speed of the car.
By division from (*) and (**),
tanθ = ac/g
ac = g tanθ
ac = (9.80 m/s2) tan15.00 = 2.63 m/s2
(b) the radius of the curve given by
r = v2/ac = (23.0 m/s)2/(2.63 m/s2) = 201 m
(c) the speed of the car if the plumb bob deflection is 9.00° while rounding the same curve, we use
tanθ = ac/g
tanθ = v2/rg
v2 = grtanθ = (9.80 m/s2)(201 m) tan9.000
v = 17.7 m/s
Problem#2
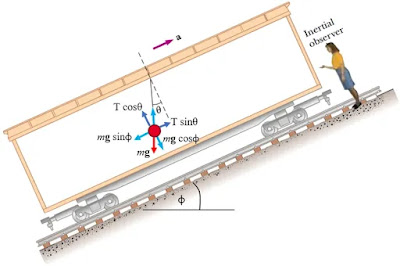
Suppose the boxcar of Figure 2 is moving with constant acceleration a up a hill that makes an angle φ with the horizontal. If the pendulum makes a constant angle θ with the perpendicular to the ceiling, what is a?
 |
| Fig.2 |
Answer:
Review the incline alignment (x-axis)
∑Fx = ma
T sinθ – mg sinφ = ma (*)
and
∑Fy = may
T cosθ – mg cosφ = 0
T = mg cosφ/cosθ
substitution (**) to (*) we get
(mg cosφ/cosθ)sinθ – mg sinφ = ma
(g sinθcosφ/cosθ)– (g cosθsinφ/cosθ) = a
a = g(sinθcosφ– cosθsinφ)/cosθ
a = gsin(θ – φ)secθ
Problem#3
(a) A luggage carousel at an airport has the form of a section of a large cone, steadily rotating about its vertical axis. Its metallic surface slopes downward toward the outside, making an angle of 20.0° with the horizontal. A piece of luggage having mass 30.0 kg is placed on the carousel, 7.46 m from the axis of rotation. The travel bag goes around once in 38.0 s. Calculate the force of static friction
between the bag and the carousel. (b) The drive motor is shifted to turn the carousel at a higher constant rate of rotation, and the piece of luggage is bumped to another position, 7.94 m from the axis of rotation. Now going around once in every 34.0 s, the bag is on the verge of slipping. Calculate the coefficient of static friction between the bag and the carousel.
 |
| Fig.4 |
Answer:
The styles that work on the bag are published in the fig.57 below
(a) With the speed of the bag is
v = s/t = (2πr)/t
v = 2π(7.46 m)/(38.0 s) = 1.23 m/s
The total force on the x-axis is the centripetal force exerted by
Fc = mac = mv2/r = (30.0 kg)(1.23 m/s)2/(7.46 m) = 6.12 N
Then by using Newton's second law we get
∑Fx = mac
–nsin 20.00 + f cos 20.00 = mac = 6.12 N
n = (f cos20.00 – 6.12 N)/sin 20.00 (*)
∑Fy = 0
f sin 20.00 + ncos 20.00 – mg = 0
f sin20.00 + ncos20.00 = (30.0 kg)(9.80 m/s2)
f sin20.00 + ncos20.00 = 294 N (**)
from (*) and (**) we get
f sin20.00 + [(f cos20.00 – 6.12 N)/sin 20.00]cos20.00 = 294 N
f sin20.00 + fsec20.00cos20.00
2.92f – 16.8 N = 294 N
f = 310.8 N/2.92 = 106 N
(b) the speed of the bag is
v = s/t = (2πr)/t
v = 2π(7.94 m)/(34.0 s) = 1.47 m/s
The total force on the x-axis is the centripetal force exerted by
Fc = mac = mv2/r = (30.0 kg)(1.47 m/s)2/(7.94 m) = 8.13 N
Then by using Newton's second law we get
∑Fx = mac
–nsin 20.00 + f cos 20.00 = mac = 8.13 N
n = (f cos20.00 – 6.12 N)/sin 20.00 (*)
∑Fy = 0
f sin 20.00 + ncos 20.00 – mg = 0
f sin20.00 + ncos20.00 = (30.0 kg)(9.80 m/s2)
f sin20.00 + ncos20.00 = 294 N (**)
from (*) and (**) we get
f sin20.00 + [(f cos20.00 – 8.13 N)/sin 20.00]cos20.00 = 294 N
f sin20.00 + fsec20.00cos20.00
2.92f – 22.4 N = 294 N
f = 316.4 N/2.92 = 108 N
then, fro, (*), we get
n = (108N cos20.00 – 6.12 N)/sin 20.00 = 273 N
So, the coefficient of static friction between the bag and the carousel is
µs = f/n = 108 N/273 N
µs = 0.396
Problem#4
Because the Earth rotates about its axis, a point on the equator experiences a centripetal acceleration of 0.033 7 m/s2, while a point at the poles experiences no centripetal acceleration. (a) Show that at the equator the gravitational force on an object must exceed the normal force required to support the object. That is, show that the object’s true weight exceeds its apparent weight. (b) What is the apparent weight at the equator and at the poles of a person having a mass of 75.0 kg? (Assume the Earth is a uniform sphere and take g = 9.800 m/s2.)
Answer:
(a) Since the centripetal acceleration of a person is downward (toward the axis of the earth), it is equivalent to the effect of a fallingelevator. Therefore,
mg' = mg – mv2/r
or mg’ < mg
(b) At the poles v = 0 and mg’ = mg = 75 kg x 9.80 m/s2 = 735 N(down)
At the equator,
mg’ = mg – mac
mg’ = 735 N – 75 kg(0.0337 m/s2) = 732 N (down)



Post a Comment for "Circular Motion and Other Applications of Newton’s Laws Additional Problems and Solutions 2"