Problem#1
In Fig. 1, two semicircular arcs have radius R2 = 7.80 cm and R1 = 3.15 cm, carry current i = 0.281 A, and have the same center of curvature C.What are the (a) magnitude and (b) direction (into or out of the page) of the net magnetic field at C?
 |
| Fig.1 |
Answer:
We will break the given shape into four pieces. Then, for each piece, we find its contribution to the magnetic field at C.
The net magnetic field Bnet at C it simply the (vector) sum of the (four) contributions. Recall that radial segments (1 and 3) do not contribute any magnetic field.
 |
| Fig.3 |
Therefore, we only need to focus on 2 and 4. They are circular arcs whose magnetic fields at the center ca be found by
B = μ0iθ/4πR
The directions of the magnetic fields are determined by the curled─straight right─hand rule.
Applying the rule, we found that at C, arc 2 gives B2 which points out the page and arc 4 gives B2 which points into the page.
(a) the net B is given by
Bnet = B4 ─ B2 = μ0iθ/4πR1 ─ μ0iθ/4πR2
Bnet = [μ0iθ/4π][1/R1 ─ 1/R2]
Bnet = [(4π x 10─7 T.m/A)(0.281 A)(π)/4π][1/0.315 m ─ 1/0.780 m]
Bnet = 1.67 x 10─7 T
(b) note that B4 > B2, hence the net B will point into of the page
Problem#2
In Fig. 4, a wire forms a semicircle of radius R = 9.26 cm and two (radial) straight segments each of length L = 13.1 cm. The wire carries current i = 34.8 mA. What are the (a) magnitude and (b) direction (into or out of the page) of the net magnetic field at the semicircle’s center of curvature C?
 |
| Fig.4 |
Answer:
(a) we see that the current in the straight segments collinear with C do not contribute to the field at that point.
B = μ0iφ/4πR (Center of circular are)
Indicates that the current in the semicircular arc (with φ = π) contributes B = µ0i/4R to the field at C.
Thus, the magnitude of the magnetic field is
BC = µ0i/4R = (4π x 10─7 T.m/A)(0.0348A)/(4 x 0.0926 m)
BC = 1.18 x 10─7 T
(b) The right-hand rule shows that this field is into the page.
Problem#3
Figure 5 shows two current segments. The lower segment carries a current of i1 = 0.40 A and includes a semicircular arc with radius 5.0 cm, angle 180°, and center point P. The upper segment carries current i2 = 2i1 and includes a circular arc with radius 4.0 cm, angle 120°, and the same center point P. What are the (a) magnitude and (b) direction of the net magnetic field B at P for the indicated current directions? What are the (c) magnitude and (d) direction B of if i1 is reversed?
 |
| Fig.5 |
Answer:
Recall that radial segments (3, 4, 5, and 6) do not contribute any magnetic field. Therefore, we only need to focus on the circular arcs.
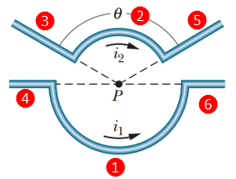 |
| Fig.6 |
1 and 2 are circular arcs whose magnetic fields at the center ca be found by
B = μ0iθ/4πR
Applying the rule, we found that at P, arc 1 gives B1 which points out the page and arc 2 gives B2 which points into the page.
Also,
B1 = μ0i1π/4πR = (4π x 10─7 T.m/A)(0.4A)/(4 x 0.05 m) = 8π x 10─7 T and
B2 = μ0i2(2π/3)/4πR = (4π x 10─7 T.m/A)(2/3)(0.8A)/(4 x 0.04 m) = 13.2π x 10─7 T
Therefore,
Bnet = B2 ─ B1 = 13.2π x 10─7 T ─ 8π x 10─7 T = 1.68 x 10─6 T
(b) note that B2 > B1, hence the net B will point into of the page
(c) B1 and B2 are now in the same direction. Therefore,
Bnet = B2 + B1 = 13.2π x 10─7 T + 8π x 10─7 T = 6.7 x 10─6 T
(c) the direction of B1 and B2 are both into the page. Therefore, the direction of Bnet = B1 + B2 is also into the page.
Problem#4
In Fig. 7, two concentric circular loops of wire carrying current in the same direction lie in the same plane. Loop 1 has radius 1.50 cm and carries 4.00 mA. Loop 2 has radius 2.50 cm and carries 6.00 mA. Loop 2 is to be rotated about a diameter while the net magnetic field set up by the two loops at their common center is measured. Through what angle must loop 2 be rotated so that the magnitude of that net field is 100 nT?
 |
| Fig.7 |
Answer:
The magnitude of the magnetic field at the center of a circular arc, of radius R and central angle φ (in radians), carrying current i, is
B = μ0iφ/4πR, with φ = 2π, then
B = μ0i/2R
 |
| Fig.8 |
For loop 2:
B2 = μ0i2/2R2 = (4π x 10─7 T.m/A)(6.00 x 10─3 A)/(2 x 0.025 m) = 1.51 x 10─7 T
The net B field:
Bnet2 = B12 + B22 + 2B1B2 cos θ
(10─7)2 = (1.67 x 10─7 T)2 + (1.51 x 10─7 T)2 + 2(1.67 x 10─7 T)(1.51 x 10─7 T) cos θ
1 = 5.069 + 5.0434 cos θ
cos θ = ─4.069/5.0434
θ = arc cos (─0.8068) ≈ 1440
Post a Comment for "Magnetic Field Due to a Current in a Circular Arc of Wire Problems and Solutions 2"