Problem#1
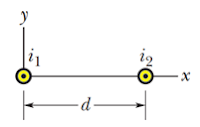
In Fig. 1, two long straight wires at separation d = 16.0 cm carry currents i1 = 3.61 mA and i2 3.00i1 out of the page. (a) Where on the x axis is the net magnetic field equal to zero? (b) If the two currents are doubled, is the zero-field point shifted toward wire 1, shifted toward wire 2, or unchanged?
Answer:
B net can only equal zero between the two wires, B1 point upwards and B2 point downward.
Bnet = B1 – B2 = 0
Or, B1 = B2
μ0i1/2πr1 = μ0i2/2πr2
i1/r = 3.00i1/(d – r)
3r = d – r
r = d/4 = 16.0 cm/4 = 4.00 cm
so, when B = 0 at r = 4.00 cm
B net can only equal zero between the two wires, B1 point upwards and B2 point downward.
Bnet = B1 – B2 = 0
Or, B1 = B2
μ0i1/2πr1 = μ0i2/2πr2
i1/r = 3.00i1/(d – r)
3r = d – r
r = d/4 = 16.0 cm/4 = 4.00 cm
so, when B = 0 at r = 4.00 cm
 |
| Fig.2 |
As long as i2 = 3.00i1 the location of Bnet = 0 doesn’t change.
Problem#2
In Fig. 3, point P2 is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P1 due to i?
Answer:
Consider the Biot-Savart law in differential form:
dB = (μ0 ids x r)/(4πr3), with dB from all segments of wire point out of page.
dB = (μ0 ids sin θ)/(4πr2)
B = (μ0i/4π)∫[ds sin θ/r2]
Consider the Biot-Savart law in differential form:
dB = (μ0 ids x r)/(4πr3), with dB from all segments of wire point out of page.
dB = (μ0 ids sin θ)/(4πr2)
B = (μ0i/4π)∫[ds sin θ/r2]
With ds → dx and r2 = R2 + x2, then sin θ = R/(R2 + x2)1/2
Known:
L = 0.18 m, R = 0.131 m and i = 0.0582 A, then
B = 5.03 x 10-8 T = 50.3 nT, out of page
Problem#3
In Fig. 5, point P2 is at distance R = 25.1 cm from one end of a straight wire of length L = 13.6 cm carrying current i = 0.693 A. (Note that the wire is not long.) What is the magnitude of the magnetic field at P2?
Answer:
Consider the Biot-Savart law in differential form:
dB = (μ0 ids x r)/(4πr3), with dB from all segments of wire point out of page.
dB = (μ0 ids sin θ)/(4πr2)
B = (μ0i/4π)∫[ds sin θ/r2]
With ds → dx and r2 = R2 + x2, then sin θ = R/(R2 + x2)1/2
Known:
L = 0.18 m, R = 0.131 m and i = 0.0582 A, then
B = 1.32 x 10-8 T = 132 nT, out of page
Problem#4
Figure 5 shows two very long straight wires (in cross section) that each carry a current of 4.00 A directly out of the page. Distance d1 = 6.00 m and distance d2 = 4.00 m. What is the magnitude of the net magnetic field at point P, which lies on a perpendicular bisector to the wires?
Answer:
The magnitude of the magnetic field at point P due to two wires is
BP = B1 sin α + B2 sin α
Known:
L = 0.18 m, R = 0.131 m and i = 0.0582 A, then
B = 5.03 x 10-8 T = 50.3 nT, out of page
Problem#3
In Fig. 5, point P2 is at distance R = 25.1 cm from one end of a straight wire of length L = 13.6 cm carrying current i = 0.693 A. (Note that the wire is not long.) What is the magnitude of the magnetic field at P2?
Answer:
Consider the Biot-Savart law in differential form:
dB = (μ0 ids x r)/(4πr3), with dB from all segments of wire point out of page.
dB = (μ0 ids sin θ)/(4πr2)
B = (μ0i/4π)∫[ds sin θ/r2]
With ds → dx and r2 = R2 + x2, then sin θ = R/(R2 + x2)1/2
Known:
L = 0.18 m, R = 0.131 m and i = 0.0582 A, then
B = 1.32 x 10-8 T = 132 nT, out of page
Problem#4
Figure 5 shows two very long straight wires (in cross section) that each carry a current of 4.00 A directly out of the page. Distance d1 = 6.00 m and distance d2 = 4.00 m. What is the magnitude of the net magnetic field at point P, which lies on a perpendicular bisector to the wires?
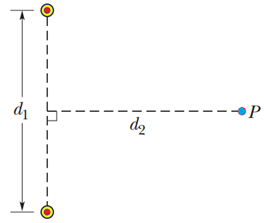 |
| Fig.5 |
The magnitude of the magnetic field at point P due to two wires is
BP = B1 sin α + B2 sin α
with the magnitude of the magnetic field each wire at point P is
B1 = B2 = μ0i/2πr
Then
BP = (μ0i/πr)sin α
from the figure we know
tan θ = ¾ or θ = 36.90, so that α = 90 ─ 36.9 = 53.10
so
BP = [(4π x 10-7 Wb/A.m)(4.00 A)/(2π x 5.00 m)] sin 53.1
BP = 5.12 x 10─8 T upward
B1 = B2 = μ0i/2πr
Then
BP = (μ0i/πr)sin α
from the figure we know
tan θ = ¾ or θ = 36.90, so that α = 90 ─ 36.9 = 53.10
so
BP = [(4π x 10-7 Wb/A.m)(4.00 A)/(2π x 5.00 m)] sin 53.1
BP = 5.12 x 10─8 T upward



Post a Comment for "Magnetic Field Due to a Current in a Long Straight Wire Problems and Solutions 2"