Problem#1
Figure 9a shows, in cross section, two long, parallel wires carrying current and separated by distance L. The ratio i1/i2 of their currents is 4.00; the directions of the currents are not indicated. Figure 9b shows the y component By of their net magnetic field along the x axis to the right of wire 2. The vertical scale is set by Bys = 4.0 nT, and the horizontal scale is set by xs = 20.0 cm. (a) At what value of x > 0 is By maximum? (b) If i2 = 3 mA, what is the value of that maximum? What is the direction (into or out of the page) of (c) i1 and (d) i2?B = 0 at x = 10 cm, so i1 and i2 are in opposite directions:
Bnet = μ0i1/[2π(L + x)] ─ μ0i2/2πx
Bnet = μ04i2/[2π(L + x)] ─ μ0i2/2πx
Bnet = [μ0i2/2π][4/(L + x)] ─ 1/x]
B is maximum when x matches the following equation:
dBnet/dx = 0
d[4/(L + x)] ─ 1/x]/dx = 0
─3x2 + 2Lx + L2 = 0
(x ─ L)(3x + L) = 0
x = L or x = ─L/3 (discarded as x < 0)
Now, we need to calculate L. At x = 10 cm, By = 0, so:
3x - L = 0 → L = 3x = 30(cm)
(b) if i2 = 3 mA:
Bnet,max = [μ0i2/2π][4/(L + L)] ─ 1/L]
Bnet,max = μ0i2/2πL
Bnet,max = (4π x 10-7 Wb/A.m)(0.003 A)/(2π x 0.3 m) = 2 nT
(c), (d): for x > 10 cm, Bnet > 0, and B1 > B2 : so B1 > 0 and B2 < 0, thus i1 is directed out and i2 into
the page
Problem#2
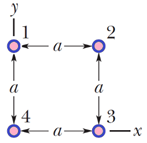
In Fig. 10, four long straight wires are perpendicular to the page, and their cross sections form a square of edge length a = 20 cm. The currents are out of the page in wires 1 and 4 and into the page in wires 2 and 3, and each wire carries 20 A. In unit-vector notation, what is the net magnetic field at the square’s center?
Answer:
Each wire produces a field with magnitude given by
B = µ0i/2πr,
where r is the distance from the corner of the square to the center.
According to the Pythagorean theorem, the diagonal of the square has length √(2a) , so r = a/√2 then
B = µ0i/(πa√2)
The fields due to the wires at the upper left and lower right corners both point toward the upper right corner of the square. The fields due to the wires at the upper right and lower left corners both point toward the upper left corner. The horizontal components cancel and the vertical components sum to
Bnet = 4B cos 450 = 4µ0i cos 450/(πa√2)
Bnet = 2µ0i/πa
Bnet = 2(4π x 10-7 Wb/A.m)(20 A)/(π x 0.20 m) = 8.0 x 10-5 T
In the calculation cos 45° was replaced with 1/√2 . The total field points upward, or in the +y direction. Thus,
Bnet = (8.0 x 10-5 T)j
Problem#3
In Fig. 11, two long straight wires (shown in cross section) carry the currents i1 = 30.0 mA and i2 = 40.0 mA directly out of the page. They are equal distances from the origin, where they set up a magnetic field .To what value must current i1 be changed in order to rotate 20.0° clockwise?
Answer:
We use
B = µ0i/2πr
to relate the magnitudes of the magnetic fields B1 and B2 to the currents (i1 and i2, respectively) in the two long wires. The angle of their net field is
tan θ = B2/B1 = i2/i1
tan θ = 40.0 mA/30.0 mA
θ = tan─1(4/3) = 53.10
The accomplish the net field rotation described in the problem, we must achieve a final angle
θ’ = 53.10 ─ 200 = 33.10
Thus, the final value for the
tan θ’ = i2/i1
tan 33.10 = 40.0 mA/i1
i1 = 40.0 mA/tan 33.10 = 61.3 mA
Problem#4
In Fig. 12, length a is 4.7 cm (short) and current i is 13 A.What are the (a) magnitude and (b) direction (into or out of the page) of the magnetic field at point P?
Answer:
For wire 1 and wire 4, ds × r = 0 , so there is no contribution to the field from this segment.
The magnitude of the 5 wire magnetic field and wire 6 there is a point P equal to that is
B5 = B6 = [µ0i/4πr][cos 450 ─ cos 2700] = [µ0i/8πa][cos 450 ─ cos 2700]
B56 = µ0i√2/16πa
The magnitude of the 2 wire magnetic field and wire 3 there is a point P equal to that is
B2 = B3 = [µ0i/4πr][cos 450 ─ cos 2700] = [µ0i/4πa][cos 450 ─ cos 2700]
B23 = µ0i√2/8πa
So the total field is
Bnet = B2 + B3 + B5 + B6
Bnet = B2 (into page) + B3 (into page) + B5 (out page) + B6 (out page)
= µ0i√2/8πa + µ0i√2/8πa ─ µ0i√2/16πa ─ µ0i√2/16πa
Bnet = µ0i√2/8πa (into page)
= (4π x 10-7 Wb/A.m)(13 A)√2/(8π x 0.047 m)
Bnet = 195.58 x 10-7 T ≈ 20 μT (into page)
Bnet = μ0i1/[2π(L + x)] ─ μ0i2/2πx
Bnet = μ04i2/[2π(L + x)] ─ μ0i2/2πx
Bnet = [μ0i2/2π][4/(L + x)] ─ 1/x]
B is maximum when x matches the following equation:
dBnet/dx = 0
d[4/(L + x)] ─ 1/x]/dx = 0
─3x2 + 2Lx + L2 = 0
(x ─ L)(3x + L) = 0
x = L or x = ─L/3 (discarded as x < 0)
Now, we need to calculate L. At x = 10 cm, By = 0, so:
3x - L = 0 → L = 3x = 30(cm)
(b) if i2 = 3 mA:
Bnet,max = [μ0i2/2π][4/(L + L)] ─ 1/L]
Bnet,max = μ0i2/2πL
Bnet,max = (4π x 10-7 Wb/A.m)(0.003 A)/(2π x 0.3 m) = 2 nT
(c), (d): for x > 10 cm, Bnet > 0, and B1 > B2 : so B1 > 0 and B2 < 0, thus i1 is directed out and i2 into
the page
Problem#2
In Fig. 10, four long straight wires are perpendicular to the page, and their cross sections form a square of edge length a = 20 cm. The currents are out of the page in wires 1 and 4 and into the page in wires 2 and 3, and each wire carries 20 A. In unit-vector notation, what is the net magnetic field at the square’s center?
 |
| Fig.10 |
Each wire produces a field with magnitude given by
B = µ0i/2πr,
where r is the distance from the corner of the square to the center.
According to the Pythagorean theorem, the diagonal of the square has length √(2a) , so r = a/√2 then
B = µ0i/(πa√2)
The fields due to the wires at the upper left and lower right corners both point toward the upper right corner of the square. The fields due to the wires at the upper right and lower left corners both point toward the upper left corner. The horizontal components cancel and the vertical components sum to
Bnet = 4B cos 450 = 4µ0i cos 450/(πa√2)
Bnet = 2µ0i/πa
Bnet = 2(4π x 10-7 Wb/A.m)(20 A)/(π x 0.20 m) = 8.0 x 10-5 T
In the calculation cos 45° was replaced with 1/√2 . The total field points upward, or in the +y direction. Thus,
Bnet = (8.0 x 10-5 T)j
Problem#3
In Fig. 11, two long straight wires (shown in cross section) carry the currents i1 = 30.0 mA and i2 = 40.0 mA directly out of the page. They are equal distances from the origin, where they set up a magnetic field .To what value must current i1 be changed in order to rotate 20.0° clockwise?
 |
| Fig.11 |
We use
B = µ0i/2πr
to relate the magnitudes of the magnetic fields B1 and B2 to the currents (i1 and i2, respectively) in the two long wires. The angle of their net field is
tan θ = B2/B1 = i2/i1
tan θ = 40.0 mA/30.0 mA
θ = tan─1(4/3) = 53.10
The accomplish the net field rotation described in the problem, we must achieve a final angle
θ’ = 53.10 ─ 200 = 33.10
Thus, the final value for the
tan θ’ = i2/i1
tan 33.10 = 40.0 mA/i1
i1 = 40.0 mA/tan 33.10 = 61.3 mA
Problem#4
In Fig. 12, length a is 4.7 cm (short) and current i is 13 A.What are the (a) magnitude and (b) direction (into or out of the page) of the magnetic field at point P?
 |
| Fig.12 |
For wire 1 and wire 4, ds × r = 0 , so there is no contribution to the field from this segment.
The magnitude of the 5 wire magnetic field and wire 6 there is a point P equal to that is
B5 = B6 = [µ0i/4πr][cos 450 ─ cos 2700] = [µ0i/8πa][cos 450 ─ cos 2700]
B56 = µ0i√2/16πa
The magnitude of the 2 wire magnetic field and wire 3 there is a point P equal to that is
B2 = B3 = [µ0i/4πr][cos 450 ─ cos 2700] = [µ0i/4πa][cos 450 ─ cos 2700]
B23 = µ0i√2/8πa
 |
| Fig.13 |
Bnet = B2 + B3 + B5 + B6
Bnet = B2 (into page) + B3 (into page) + B5 (out page) + B6 (out page)
= µ0i√2/8πa + µ0i√2/8πa ─ µ0i√2/16πa ─ µ0i√2/16πa
Bnet = µ0i√2/8πa (into page)
= (4π x 10-7 Wb/A.m)(13 A)√2/(8π x 0.047 m)
Bnet = 195.58 x 10-7 T ≈ 20 μT (into page)

Post a Comment for "Magnetic Field Due to a Current in a Long Straight Wire Problems and Solutions 3"