Problem#1
A thin, 50.0-cm-long metal bar with mass 750 g rests on, but is not attached to, two metallic supports in a uniform 0.450-T magnetic field, as shown in Fig. 1. A battery and a 25.0 Ω resistor in series are connected to the supports. (a) What is the highest voltage the battery can have without breaking the circuit at the supports? (b) The battery voltage has the maximum value calculated in part (a). If the resistor suddenly gets partially short-circuited, decreasing its resistance to 2.0 Ω find the initial acceleration of the bar.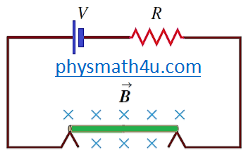 |
| Fig.1 |
Answer:
Known:
magnetic field, B = 0.450 T
mass, m = 750 g = 0.75 kg
length metal, L = 50 cm = 0.50 m
(a) The current flowing to the right in the bar feels a lifting force from the magnetic field FB = IL × B which balances the gravitational force Fg = mg. Because the current and magnetic field are perpendicular to each other, we can focus on the magnitudes
F = ILB sin θ = Fg = mg
I = mg/(LB sin θ), θ = 900
I = (0.75 kg)(9.80 m/s2)/[0.50 m x 0.450 T] = 32.7 A
This maximum current would occur when the voltage V from the battery balanced an IR drop across the resistor,
so V = IR = 32.7 A x 25.0 Ω = 817 V
(b) When the resistor shorts, the current jumps to I’ = V/R’, because the resistor voltage still has to match the battery voltage. This creates a net lifting force and acceleration on the bar.
F = FB − Fg
I’LB − mg = VLB/R’ − mg = ma
817 V x 0.5 m x 0.45 T/2.00 Ω – 0.750 kg x 9.80 m/s2 = 0.750 kg x a
a = 84.5625/0.75 = 112.75 m/s2
Problem#2
The circuit shown in Fig. 2 is used to make a magnetic balance to weigh objects. The mass m to be measured is hung from the center of the bar that is in a uniform magnetic field of 1.50 T, directed into the plane of the figure. The battery voltage can be adjusted to vary the current in the circuit. The horizontal bar is 60.0 cm long and is made of extremely light-weight material. It is connected to the battery by thin vertical wires that can support no appreciable tension; all the weight of the suspended mass m is supported by the magnetic force on the bar. A resistor with R = 5.00 Ω is in series with the bar; the resistance of the rest of the circuit is much less than this. (a) Which point, a or b should be the positive terminal of the battery? (b) If the maximum terminal voltage of the battery is 175 V, what is the greatest mass m that this instrument can measure?
magnetic field, B = 0.450 T
mass, m = 750 g = 0.75 kg
length metal, L = 50 cm = 0.50 m
(a) The current flowing to the right in the bar feels a lifting force from the magnetic field FB = IL × B which balances the gravitational force Fg = mg. Because the current and magnetic field are perpendicular to each other, we can focus on the magnitudes
F = ILB sin θ = Fg = mg
I = mg/(LB sin θ), θ = 900
I = (0.75 kg)(9.80 m/s2)/[0.50 m x 0.450 T] = 32.7 A
This maximum current would occur when the voltage V from the battery balanced an IR drop across the resistor,
so V = IR = 32.7 A x 25.0 Ω = 817 V
(b) When the resistor shorts, the current jumps to I’ = V/R’, because the resistor voltage still has to match the battery voltage. This creates a net lifting force and acceleration on the bar.
F = FB − Fg
I’LB − mg = VLB/R’ − mg = ma
817 V x 0.5 m x 0.45 T/2.00 Ω – 0.750 kg x 9.80 m/s2 = 0.750 kg x a
a = 84.5625/0.75 = 112.75 m/s2
Problem#2
The circuit shown in Fig. 2 is used to make a magnetic balance to weigh objects. The mass m to be measured is hung from the center of the bar that is in a uniform magnetic field of 1.50 T, directed into the plane of the figure. The battery voltage can be adjusted to vary the current in the circuit. The horizontal bar is 60.0 cm long and is made of extremely light-weight material. It is connected to the battery by thin vertical wires that can support no appreciable tension; all the weight of the suspended mass m is supported by the magnetic force on the bar. A resistor with R = 5.00 Ω is in series with the bar; the resistance of the rest of the circuit is much less than this. (a) Which point, a or b should be the positive terminal of the battery? (b) If the maximum terminal voltage of the battery is 175 V, what is the greatest mass m that this instrument can measure?
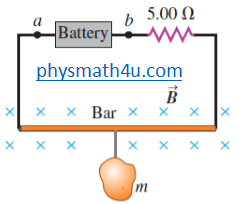 |
| Fig.2 |
Answer:
Known:
magnetic field, B = 1.50 T
length metal, L = 60 cm = 0.60 m
voltage, V = 175 V
resistor, R = 5.00 Ω
The magnetic force FB must be upward and equal to mg. The direction of FB is determined by the direction of I in the circuit.
FB = ILB sin φ, with φ = 900, I = V/R, where V is the battery voltage.
(a) The forces are shown in the figure below. The current Iin the bar must be to the right to produce FB upward. To produce current in this direction, point a must be the positive terminal of the battery.
(b) FB = mg
ILB = mg
m = ILB/g = VLB/gR
m = (175 V)(0.60 m)(1.50 T)/[9.8 m/s2 x 5.00 Ω]
m = 3.21 kg
Problem#3
A 2.60 N metal bar, 1.50 m long and having a resistance of 10.0 Ω, rests horizontally on conducting wires connecting it to the circuit shown in Fig. 3. The bar is in a uniform, horizontal, 1.60 T magnetic field and is not attached to the wires in the circuit. What is the acceleration of the bar just after the switch S is closed?
magnetic field, B = 1.50 T
length metal, L = 60 cm = 0.60 m
voltage, V = 175 V
resistor, R = 5.00 Ω
The magnetic force FB must be upward and equal to mg. The direction of FB is determined by the direction of I in the circuit.
FB = ILB sin φ, with φ = 900, I = V/R, where V is the battery voltage.
(a) The forces are shown in the figure below. The current Iin the bar must be to the right to produce FB upward. To produce current in this direction, point a must be the positive terminal of the battery.
(b) FB = mg
ILB = mg
m = ILB/g = VLB/gR
m = (175 V)(0.60 m)(1.50 T)/[9.8 m/s2 x 5.00 Ω]
m = 3.21 kg
Problem#3
A 2.60 N metal bar, 1.50 m long and having a resistance of 10.0 Ω, rests horizontally on conducting wires connecting it to the circuit shown in Fig. 3. The bar is in a uniform, horizontal, 1.60 T magnetic field and is not attached to the wires in the circuit. What is the acceleration of the bar just after the switch S is closed?
 |
| Fig.3 |
Answer:
Known:
magnetic field, B = 1.60 T
length metal, L = 1.50 m
voltage, V = 120.0 V
Weight metal bar, mg = 2.60 N
When S is closed, current begins to flow, creating a magnetic force FB = IbL × B on the bar, where Ib is the current through the bar. Using our cross product right-hand rule and magnitude formula, we see that the force on the bar is out of the page with a magnitude FB = IbL × B. We just need to find Ib.
Because the bar and vertical resistor are in parallel, the equivalent resistance for the vertical resistor and bar is
R’ = [1/10 Ω + 1/10 Ω]─1 = 5.0 Ω
and the resistance for the entire circuit is
R = 25.0 Ω + 5.00 Ω = 30.0 Ω
This effective resistance must drop all the voltage generated by the battery, so we can manipulate Ohm’s law V = IR to yield
I = V/R = 120.0 V/30 Ω = 4.00 A
This is the total current through the battery. Now we need to find the current through the bar. The voltage across the vertical-resistor/bar portion is
Vb = IR’= 4.00 A x 5.00 Ω = 20.0 V
and current through the bar is
Ib = Vb/Rb = 20.0 V/10.0 Ω = 2.00 A
The lifting force and acceleration are then
F = Fb − Fg
IbLB – mg = ma
2.00 A x 1.50 m x 1.60 T ─ 2.60 N = (2.60 N/9.80 m/s2)a
a = 8.29 m/s2
Note that I factored out g to mg in the denominator, because they give the weight of the bar (mg = 2.60 N), not the mass m. Obviously, you could get a number for m if you want, but keeping mg together allows us to avoid the trouble.
Problem#4
A particle of charge q > 0 is moving at speed v in the +z-direction through a region of uniform magnetic field B. The magnetic force on the particle is F = F0(3i+ 4j), where F0 is a positive constant. (a) Determine the components Bx, By, and Bz, or at least as many of the three components as is possible from the information given. (b) If it is given in addition that the magnetic field has magnitude 6F0/qv, determine as much as you can about the remaining components of B.
Answer:
(a) Writing FB = qv·B in terms of components
FB = q[i(vyBz − vzBy) − j(vxBz − vzBx) + k(vxBy − vyBx)]
FB = q(−vzBy i + vzBx j)
FB = F0(3i + 4j)
Matching components and writing vz = v we have
−qvBy = 3F0
By = −3F0/qv < 0
And
qvBx = 4F0
Bx = 4F0/qv > 0
We can’t find Bz because it does not contribute to the force felt by the charge, which is currently our only handle on B.
(b) With |B|, we can solve for |Bz|.
|B|2 = Bx2 + By2 + Bz2
Bz2 =|B|2 ─ Bx2 + By2 = (6F0/qv)2 ─ (4F0/qv)2 + (−3F0/qv)2 = 11(F0/qv)2
BZ = ±(F0/qv)√11
However, we still cannot find the direction of Bz.
magnetic field, B = 1.60 T
length metal, L = 1.50 m
voltage, V = 120.0 V
Weight metal bar, mg = 2.60 N
When S is closed, current begins to flow, creating a magnetic force FB = IbL × B on the bar, where Ib is the current through the bar. Using our cross product right-hand rule and magnitude formula, we see that the force on the bar is out of the page with a magnitude FB = IbL × B. We just need to find Ib.
Because the bar and vertical resistor are in parallel, the equivalent resistance for the vertical resistor and bar is
R’ = [1/10 Ω + 1/10 Ω]─1 = 5.0 Ω
and the resistance for the entire circuit is
R = 25.0 Ω + 5.00 Ω = 30.0 Ω
This effective resistance must drop all the voltage generated by the battery, so we can manipulate Ohm’s law V = IR to yield
I = V/R = 120.0 V/30 Ω = 4.00 A
This is the total current through the battery. Now we need to find the current through the bar. The voltage across the vertical-resistor/bar portion is
Vb = IR’= 4.00 A x 5.00 Ω = 20.0 V
and current through the bar is
Ib = Vb/Rb = 20.0 V/10.0 Ω = 2.00 A
The lifting force and acceleration are then
F = Fb − Fg
IbLB – mg = ma
2.00 A x 1.50 m x 1.60 T ─ 2.60 N = (2.60 N/9.80 m/s2)a
a = 8.29 m/s2
Note that I factored out g to mg in the denominator, because they give the weight of the bar (mg = 2.60 N), not the mass m. Obviously, you could get a number for m if you want, but keeping mg together allows us to avoid the trouble.
Problem#4
A particle of charge q > 0 is moving at speed v in the +z-direction through a region of uniform magnetic field B. The magnetic force on the particle is F = F0(3i+ 4j), where F0 is a positive constant. (a) Determine the components Bx, By, and Bz, or at least as many of the three components as is possible from the information given. (b) If it is given in addition that the magnetic field has magnitude 6F0/qv, determine as much as you can about the remaining components of B.
Answer:
(a) Writing FB = qv·B in terms of components
FB = q[i(vyBz − vzBy) − j(vxBz − vzBx) + k(vxBy − vyBx)]
FB = q(−vzBy i + vzBx j)
FB = F0(3i + 4j)
Matching components and writing vz = v we have
−qvBy = 3F0
By = −3F0/qv < 0
And
qvBx = 4F0
Bx = 4F0/qv > 0
We can’t find Bz because it does not contribute to the force felt by the charge, which is currently our only handle on B.
(b) With |B|, we can solve for |Bz|.
|B|2 = Bx2 + By2 + Bz2
Bz2 =|B|2 ─ Bx2 + By2 = (6F0/qv)2 ─ (4F0/qv)2 + (−3F0/qv)2 = 11(F0/qv)2
BZ = ±(F0/qv)√11
However, we still cannot find the direction of Bz.
Post a Comment for "Magnetic Force on a Current-Carrying Conductor Problems and Solutions 2"