Momentum and impulse Problems and Solutions

 Problem#1

A friend claims that, as long as he has his seatbelt on, he can hold on to a 12.0-kg child in a 60.0 mi/h head-on collision with a brick wall in which the car passenger compartment comes to a stop in 0.050 0 s. Show that the violent force during the collision will tear the child from his arms. A child should always be in a toddler seat secured with a seat belt in the back seat of a car.

Answer:
Given: m = 12.0 kg, v_i = 60.0 mi/h = 26.8 m/s, v_f = 0 and ∆t = 0.050 s, then

From the impulse-momentum theorem,

F_avr∆t = m∆v

the average force required to hold onto the child is

F_avr(0.050 s) = (12.0 kg)(0 – 26.8 m/s)

F_avr = –6.44 kN

Therefore, the magnitude of the needed retarding force is 6.44 kN. A person cannot exert a force of this magnitude and a safety device should be used.

Problem#2
An estimated force–time curve for a baseball struck by a bat is shown in Figure 1. From this curve, determine (a) the impulse delivered to the ball, (b) the average force exerted on the ball, and (c) the peak force exerted on the ball.

Fig.1

Answer:
(a) the impulse delivered to the ball is

I = ∫Fdt = area under curve

I = ½ (2.50 – 1.00)(10^-3 s)(18000N) = 13.5 N.s

(b) the average force exerted on the ball is

F = I/∆t = 13.5 Ns/(1.50 x 10^-3 s) = 9.00 kN

(c) the peak force exerted on the ball is from the graph, we see that F_max = 18.0 kN.

Problem#3
A ball of mass 0.150 kg is dropped from rest from a height of 1.25 m. It rebounds from the floor to reach a height of 0.960 m. What impulse was given to the ball by the floor?

Answer:
The impact speed is given by

½ mv₁² = mgy₁

v₁ = √(2gy₁) = √[2(9.80 m/s²)(1.25 m)] = 4.95 m/s (down)

and the rebound speed is given by

½ mv₂² = mgy₂

v₂ = √(2gy₂) = √[2(9.80 m/s²)(0.960 m)] = 4.34 m/s (up)

then, the impulse of the floor is the change in momentum is

I = ∆p = mv₂ – mv₁

I = (0.150 kg)[(4.34 m/s) – (–4.95 m/s)] = 1.39 kg.m/s (upward)

Problem#4
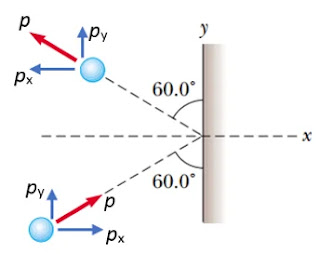
A 3.00-kg steel ball strikes a wall with a speed of 10.0 m/s at an angle of 60.0° with the surface. It bounces off with the same speed and angle (Fig. 2). If the ball is in contact with the wall for 0.200 s, what is the average force exerted by the wall on the ball ?

Answer:
We have

∆p = m∆v, then

∆p_x = m(v_fx – v_ix) = m(–vsin60.0⁰ – vsin60⁰)

∆p_x = –2(3.00 kg)(10.0 m/s)sin60.0⁰ = –52.0 kg.m/s

And
∆p_y = m(v_fy – v_iy) = m(vcos60.0⁰ – vcos60⁰) = 0

then
F_ave = ∆p_x/∆t = (–52.0 kg.m/s)/(0.200 s) = –260 N   

Share :