Problem#1
An electron at point A in Fig. 1 has a speed v0 of 1.41 x 106 m/s. Find (a) the magnitude and direction of the magnetic field that will cause the electron to follow the semicircular path from A to B and (b) the time required for the electron to move from A to B.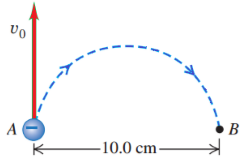 |
| Fig.1 |
Answer:
Known:
Speed, v0 = 1.41 x 106 m/s
Radius, R = 0.05 m
electron mass, me = 9.11 x 10-31 kg
(a) the magnitude of the magnetic field that will cause the electron to follow the semi-circular path from A to B will be given as:
magnetic force, Fm = centripetal Force, Fc
where, magnetic Force, Fm = ev0B and centripetal Force, Fc = mv02/R
Then,
ev0B = mv02/R
B = mv0/eR
B = (9.11 x 10-31 kg)(1.41 x 106 m/s)/[(1.60 x 10-19 C) x 0.05 m]
B = 0.16 mT (into the page)
(b) the time required for the electron to move from A to B is
tAB = πR/v0
tAB = 2π x 0.05 m/(1.41 x 106 m/s) = 1.11 x 10-7 s = 0.11 µs
Problem#2
Repeat Problem#1 for the case in which the particle is a proton rather than an electron.
Answer:
(a) B = mv0/eR
B = (1.67 x 10-27 kg)(1.41 x 106 m/s)/[(1.60 x 10-19 C) x 0.05 m]
B = 0.294 T (out of the page)
(b) the time required for the electron to move from A to B is
tAB = πR/v0
tAB = 2π x 0.05 m/(1.41 x 106 m/s) = 1.11 x 10-7 s = 0.11 µs
Problem#3
A 150-g ball containing 4.00 x 108 excess electrons is dropped into a 125-m vertical shaft. At the bottom of the shaft, the ball suddenly enters a uniform horizontal magnetic field that has magnitude 0.250 T and direction from east to west. If air resistance is negligibly small, find the magnitude and direction of the force that this magnetic field exerts on the ball just as it enters the field.
Answer:
Known:
Mass ball, m = 150 g = 0.15 kg
number of electrons, n = 4.00 x 108
then, total charge, qtotal = 4.00 x 108 x (–1.6 x 10-19 C) = –6.408 x 10-11 C
electrons dropped from y = 125 m
magnetic field that has magnitude, B = 0.250 T
speed a bottom of shaft:
½ mv2 = mgy
v = √(2gy) = √(2 x 9.8 m/s2 x 125 m) = 49.5 m/s
speed (v) is downward and magnetic field (B) is west, so v x B is on the north.
Since q < 0 F is south
the magnitude and direction of the force that this magnetic field exerts on the ball just as it enters the field given by
F = │q│vB sin θ
F = (6.408 x 10-11 C)(49.5 m/s)(0.250 T) sin 90 = 7.93 x 10-10 N, toward the south
Problem#4
An alpha particle (a He nucleus, containing two protons and two neutrons and having a mass of 6.64 x 10-27 kg traveling horizontally at 35.6 km/s enters a uniform, vertical, 1.10 T magnetic field. (a) What is the diameter of the path followed by this alpha particle? (b) What effect does the magnetic field have on the speed of the particle? (c) What are the magnitude and direction of the acceleration of the alpha particle while it is in the magnetic field? (d) Explain why the speed of the particle does not change even though an unbalanced external force acts on it.
Answer:
Known:
Mass He, m = 6.64 x 10-27 kg
Speed, v = 35.6 km/s
magnetic field, B = 1.10 T
(a) We know that a particle whose velocity isperpendicular to the magnetic field moves in a circle with constantspeed. This is because using the right hand rule (or left handrule) the force on the particle is directed along the radius ofthis circle. When force doesn't have a component parallel to themotion of an object it can't change its speed, only the directionof velocity (which is always tangential to the circle at allpoints).
Now equate the force F = mv2/R (circular motion) tothe magnetic force F = qvB Sin θ (here θ is the angle between v and B by the way)
m = mass of particle (kg), v = its velocity (m/s), R = radius of circular path (m), q = charge (C) = 1.602 x 10-19C x 2 = 3.204 x10-19 C and and B = magnetic field (T),
so mv2/R = qvB sinθ (since, θ = 900)
R = mv/qB
R = (6.64 x 10-27kg) x (35.6 x103m/s) /(3.204 x 10-19C) x (1.10 T)
R = 6.7 x10-4 m = 0.67mm
Then the diameter of the path followed by this alpha particle is d = 2R = 1.34 mm
(b) charge q moving at a speed v perpendicular to a magnetic field of strength B. If the velocity is not perpendicular to the magnetic field, then v is the component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the magnetic force is zero for motion parallel to the field. This produces a spiral motion rather than a circular one.The magnetic field has no effect on the force of the particle. The reason was stated above.
(c) We know from Newton's law that F = ma equate this to
F = qvB Sin θ = ma
a = qvB/m
a = (3.204 x 10-19 C) x (35.6 x103m/s) x (1.1 T)/(6.64 x 10-27 kg)
a = 1.56 x1012 m/s2
direction of always towards the center of the circular.
(d) the speed of the particle does not change even though an unbalanced external force acts on it because the unbalanced force doesn't have a componentparallel to the particle's velocity.
Problem#5
A particle with charge 6.40 x 10-19 C travels in a circular orbit with radius 4.68 mm due to the force exerted on it by a magnetic field with magnitude 1.65 T and perpendicular to the orbit. (a) What is the magnitude of the linear momentum p of the particle? (b) What is the magnitude of the angular momentum L of the particle?
Answer:
Known:
Charge, q = 6.40 x 10-19 C
Radius, R = 4.68 mm = 4.68 x 10-3 m
magnetic field, B = 1.65 T
(a) the magnitude of the linear momentum p of the particle
Let m be the mass of the particle; its momentum is p = mv (nonrelativistic)
The centripetal (Lorentz) force exerted by the magnetic field has magnitude
F = qvB
F is also equal to m times the centripetal acceleration v2/R
Therefore, F = mv2/R = qvB which boils down to:
mv = qBR
p = (6.40 x 10-19 C)(1.65 T)(4.68 x 10-3 m) = 4.95 x -21 kg.m/s
(b) the magnitude of the angular momentum L of the particle
Numerically, this is the above multiplied into R:
L = mvR = (4.95 x -21 kg.m/s)(4.68 x 10-3 m) = 2.32 x 10-23 kg.m2/s
Known:
Speed, v0 = 1.41 x 106 m/s
Radius, R = 0.05 m
electron mass, me = 9.11 x 10-31 kg
(a) the magnitude of the magnetic field that will cause the electron to follow the semi-circular path from A to B will be given as:
magnetic force, Fm = centripetal Force, Fc
where, magnetic Force, Fm = ev0B and centripetal Force, Fc = mv02/R
Then,
ev0B = mv02/R
B = mv0/eR
B = (9.11 x 10-31 kg)(1.41 x 106 m/s)/[(1.60 x 10-19 C) x 0.05 m]
B = 0.16 mT (into the page)
(b) the time required for the electron to move from A to B is
tAB = πR/v0
tAB = 2π x 0.05 m/(1.41 x 106 m/s) = 1.11 x 10-7 s = 0.11 µs
Problem#2
Repeat Problem#1 for the case in which the particle is a proton rather than an electron.
Answer:
(a) B = mv0/eR
B = (1.67 x 10-27 kg)(1.41 x 106 m/s)/[(1.60 x 10-19 C) x 0.05 m]
B = 0.294 T (out of the page)
(b) the time required for the electron to move from A to B is
tAB = πR/v0
tAB = 2π x 0.05 m/(1.41 x 106 m/s) = 1.11 x 10-7 s = 0.11 µs
Problem#3
A 150-g ball containing 4.00 x 108 excess electrons is dropped into a 125-m vertical shaft. At the bottom of the shaft, the ball suddenly enters a uniform horizontal magnetic field that has magnitude 0.250 T and direction from east to west. If air resistance is negligibly small, find the magnitude and direction of the force that this magnetic field exerts on the ball just as it enters the field.
Answer:
Known:
Mass ball, m = 150 g = 0.15 kg
number of electrons, n = 4.00 x 108
then, total charge, qtotal = 4.00 x 108 x (–1.6 x 10-19 C) = –6.408 x 10-11 C
electrons dropped from y = 125 m
magnetic field that has magnitude, B = 0.250 T
speed a bottom of shaft:
½ mv2 = mgy
v = √(2gy) = √(2 x 9.8 m/s2 x 125 m) = 49.5 m/s
speed (v) is downward and magnetic field (B) is west, so v x B is on the north.
Since q < 0 F is south
the magnitude and direction of the force that this magnetic field exerts on the ball just as it enters the field given by
F = │q│vB sin θ
F = (6.408 x 10-11 C)(49.5 m/s)(0.250 T) sin 90 = 7.93 x 10-10 N, toward the south
Problem#4
An alpha particle (a He nucleus, containing two protons and two neutrons and having a mass of 6.64 x 10-27 kg traveling horizontally at 35.6 km/s enters a uniform, vertical, 1.10 T magnetic field. (a) What is the diameter of the path followed by this alpha particle? (b) What effect does the magnetic field have on the speed of the particle? (c) What are the magnitude and direction of the acceleration of the alpha particle while it is in the magnetic field? (d) Explain why the speed of the particle does not change even though an unbalanced external force acts on it.
Answer:
Known:
Mass He, m = 6.64 x 10-27 kg
Speed, v = 35.6 km/s
magnetic field, B = 1.10 T
(a) We know that a particle whose velocity isperpendicular to the magnetic field moves in a circle with constantspeed. This is because using the right hand rule (or left handrule) the force on the particle is directed along the radius ofthis circle. When force doesn't have a component parallel to themotion of an object it can't change its speed, only the directionof velocity (which is always tangential to the circle at allpoints).
Now equate the force F = mv2/R (circular motion) tothe magnetic force F = qvB Sin θ (here θ is the angle between v and B by the way)
m = mass of particle (kg), v = its velocity (m/s), R = radius of circular path (m), q = charge (C) = 1.602 x 10-19C x 2 = 3.204 x10-19 C and and B = magnetic field (T),
so mv2/R = qvB sinθ (since, θ = 900)
R = mv/qB
R = (6.64 x 10-27kg) x (35.6 x103m/s) /(3.204 x 10-19C) x (1.10 T)
R = 6.7 x10-4 m = 0.67mm
Then the diameter of the path followed by this alpha particle is d = 2R = 1.34 mm
(b) charge q moving at a speed v perpendicular to a magnetic field of strength B. If the velocity is not perpendicular to the magnetic field, then v is the component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the magnetic force is zero for motion parallel to the field. This produces a spiral motion rather than a circular one.The magnetic field has no effect on the force of the particle. The reason was stated above.
(c) We know from Newton's law that F = ma equate this to
F = qvB Sin θ = ma
a = qvB/m
a = (3.204 x 10-19 C) x (35.6 x103m/s) x (1.1 T)/(6.64 x 10-27 kg)
a = 1.56 x1012 m/s2
direction of always towards the center of the circular.
(d) the speed of the particle does not change even though an unbalanced external force acts on it because the unbalanced force doesn't have a componentparallel to the particle's velocity.
Problem#5
A particle with charge 6.40 x 10-19 C travels in a circular orbit with radius 4.68 mm due to the force exerted on it by a magnetic field with magnitude 1.65 T and perpendicular to the orbit. (a) What is the magnitude of the linear momentum p of the particle? (b) What is the magnitude of the angular momentum L of the particle?
Answer:
Known:
Charge, q = 6.40 x 10-19 C
Radius, R = 4.68 mm = 4.68 x 10-3 m
magnetic field, B = 1.65 T
(a) the magnitude of the linear momentum p of the particle
Let m be the mass of the particle; its momentum is p = mv (nonrelativistic)
The centripetal (Lorentz) force exerted by the magnetic field has magnitude
F = qvB
F is also equal to m times the centripetal acceleration v2/R
Therefore, F = mv2/R = qvB which boils down to:
mv = qBR
p = (6.40 x 10-19 C)(1.65 T)(4.68 x 10-3 m) = 4.95 x -21 kg.m/s
(b) the magnitude of the angular momentum L of the particle
Numerically, this is the above multiplied into R:
L = mvR = (4.95 x -21 kg.m/s)(4.68 x 10-3 m) = 2.32 x 10-23 kg.m2/s
Post a Comment for "Motion of Charged Particles in a Magnetic Field Problems and Solutions"