Problem#1
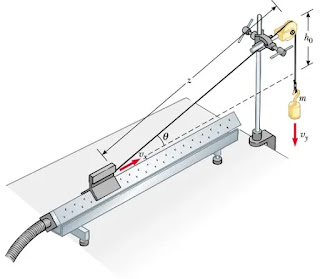
Refer to the situation described in Chapter 5, Problem 65. A 1.00-kg glider on a horizontal air track is pulled by a string at angle &. The taut string runs over a light pulley at height h0 = 40.0 cm above the line of motion of the glider. The other end of the string is attached to a hanging mass of 0.500 kg as in Fig. P5.65. (a) Show that the speed of the glider vx and the speed of the hanging mass vy are related by vy = vx cos θ. The glider is released from rest when θ = 30.0°. Find (b) vx and (c) vy when θ = 45.0°. (d) Explain why the answers to parts (b) and (c) to Chapter 5, Problem 65 do not help to solve parts (b) and (c) of this problem.
Answer:
(a) The length of string between glider and pulley is given by
l2 = x2 + h02, then
2ldl/dt = 2xdx/dt + 0
Now, dl/dt is the rate at which string goes over the pulley:
dl/dt = vy = xvx/l = (cosθ)vx
(b) we use
∆Emech = ∆K + ∆U
0 = Kf – Ki + Uf – Ui
(KA + KB + Ug)i = (KA + KB + Ug)f
0 + 0 + mBg(y30 – y45) = ½ mAvx2 + ½ mBvy2
Now y30 – y45 is the amount of string that has gone over the pulley, l30 – l45 . We have
sin300 = h0/l30 and sin450 = h0/l45, so
l30 – l45 = h0(1/sin300 – 1/sin450) = 0.40 m(2 – √2) = 0.234 m
From the energy equation
(0.500 kg)(9.80 m/s2)(0.234 m) = ½ (1.00 kg)vx2 + ½ (0.500 kg)(vx2)cos2450
1.15 J = 0.625vx2
vx = 1.35 m/s
(c) vy = vx cosθ = (1.35 m/s) cos450 = 0.958 m/s
(d) The acceleration of neither glider is constant, so knowing distance and acceleration at one
point is not sufficient to find speed at another point.
Problem#2
Jane, whose mass is 50.0 kg, needs to swing across a river (having width D) filled with man-eating crocodiles to save Tarzan from danger. She must swing into a wind exerting constant horizontal force F, on a vine having length L and initially making an angle & with the vertical (Fig. 2).Taking D = 50.0 m, F = 110 N, L = 40.0 m, and θ = 50.0°, (a) with what minimum speed must Jane begin her swing in order to just make it to the other sid? (b) Once the rescue is complete, Tarzan and Jane must swing back acrossthe river. With what minimum speed must they begin their swing? Assume that Tarzan has a mass of 80.0 kg.
Answer:
The geometry reveals D = L sinθ + Lsinφ,
(a) From takeoff to alighting for the Jane-Earth system
∆Emech = ∆K + ∆U
Wwind = Kf – Ki + Uf – Ui
–FD = 0 – ½ mvi2 + mg(–L cosφ) – mg(–L cosθ)
FD = ½ mvi2 + mg(L cosφ) – mg(L cosθ)
(110 N)(50 m) = ½ (50.0 kg)vi2 + (50.0 kg)(9.80 m/s2)(40 m cos28.90) – (50.0kg)(9.80 m/s2)(40 mcos500)
5.50 x 103 J = 25.0kgvi2 + (1.72 x 104 J) – (1.26 x 104 J)
947 J = 25.0kgvi2
vi = 6.15 m/s
(b) For the swing back
∆Emech = ∆K + ∆U
Wwind = Kf – Ki + Uf – Ui
+FD = 0 – ½ mvi2 + mg(–L cosθ) – mg(–L cosφ)
FD = –½ mvi2 – mg(L cosθ) + mg(L cosφ)
(110 N)(50 m) = –½ (130kg)vi2 – (130 kg)(9.80 m/s2)(40 m cos50.00) + (130kg)(9.80 m/s2)(40 mcos28.90)
5.50 x 103 J = –65.0kgvi2 – (3.28 x 104 J) + (4.46 x 104 J)
6340 J = 65.0kgvi2
vi = 9.87 m/s
Problem#3
A 5.00-kg block free to move on a horizontal, frictionless surface is attached to one end of a light horizontal spring. The other end of the spring is held fixed. The spring is compressed 0.100 m from equilibrium and released. The speed of the block is 1.20 m/s when it passes the equilibrium position of the spring. The same experiment is now repeated with the frictionless surface replaced by a surface for which the coefficient of kinetic friction is 0.300. Determine the speed of the block at the equilibrium position of the spring.
Answer:
If surface is frictionless
½ mv2 = ½ kx2
(5.00 kg)(1.20 m/s)2 = k(10-2 m2)
k = 7.20 x 102 N/m
If surface is rough, for µk = 0.300, then
½ mv2 = ½ kx2 – µkmgx
½ (5.00 kg)v2 = ½ (7.20 x 102 N/m)(10-1 m)2 – (0.300)(5.00 kg)(9.80 m/s2)(10-1 m)
v = 0.923 m/s

Post a Comment for "Potential Energy Additional Problems and Solutions 5"