Problem#1
A skateboarder with his board can be modeled as a particle of mass 76.0 kg, located at his center of mass (which we will study in Chapter 9). As in Figure 1, the skateboarder starts from rest in a crouching position at one lip of a half-pipe (point A). The half-pipe is a dry water channel, forming one half of a cylinder of radius 6.80 m with its axis horizontal. On his descent, the skateboarder moves without friction so that his center of mass moves through one quarter of a circle of radius 6.30 m. (a) Find his speed at the bottom of the half-pipe (point B). (b) Find his centripetal acceleration. (c) Find the normal force nB acting on the skateboarder at point B. Immediately after passing point B, he stands up and raises his arms, lifting his center of mass from 0.500 m to 0.950 m above the concrete (point C). To account for the conversion of chemical into mechanical energy, model his legs as doing work by pushing him vertically up, with a constant force equal to the normal force nB, over a distance of 0.450 m. (You will be able to solve this problem with a more accurate model in Chapter 11.) (d) What is the work done on the skateboarder’s body in this process? Next, the skateboarder glides upward with his center of mass moving in a quarter circle of radius 5.85 m. His body is horizontal when he passes point D, the far lip of the half-pipe. (e) Find his speed at this location. At last he goes ballistic, twisting around while his center of mass moves vertically. (f) How high above point D does he rise? (g) Over what time interval is he airborne before he touches down, 2.34 m below the level of point D? [Caution: Do not try this yourself without the required skill and protective equipment, or in a drainage channel to which you do not have legal access.]
 |
| Fig.1 |
Answer:
(a) Kecepatan di bagian bawah setengah pipa (titik B), we use
∆Emech = ∆K + ∆U
0 = KB – KA + UB – UA
0 = ½ mvB2 – 0 + 0 – mgyA
½vB2 = (9.80 m/s2)(6.30 m)
vB = 11.1 m/s
(b) Centripetal acceleration is
ac = v2/r = (11.1 m/s)2/(6.30 m) = 19.6 m/s2 up
(c) the normal force nB acting on the skateboarder at point B is
∑Fy = mac
n – mg = mac
n = (76.0 kg)(9.80 m/s2 + 19.6 m/s2) = 2.23 x 103 N up
(d) the work done on the skateboarder’s body in this process is
W = F∆rcosθ = (2.23 x 103 N)(0.450 m)cos00 = 1.01 x 103 J
(e) ∆Emech = ∆K + ∆U
W = KD – KB + UD – UB
W = ½ mvD2 – ½ mvB2 + mg(yD – yB)
1.01 x 103 J = ½ (76.0 kg)vD2 – ½ (76.0 kg)(11.1 m/s)2 + (76.0 kg)(9.80 m/s2)(6.30 m)
1.01 x 103 J = ½ (76.0 kg)vD2 – 4.68 x 103 J + 4.69 x 103 J
2.02 x 103 J = (76.0 kg)vD2
vD = 5.14 m/s
(f) ∆Emech = ∆K + ∆U
0 = KE – KD + UE – UD, where E is the apex of his motion
0 = 0 – ½ mvD2 + mg(yE – yD)
½ (5.14 m/s)2 = (9.80 m/s2)(yE – yD)
(yE – yD) = 1.35 m
(g) Consider the motion with constant acceleration between takeoff and touchdown. The time
is the positive root of
yf = yi + vyit + ½ ayt2
–2.34 m = 0 + (5.14 m/s)t + ½(–9.80 m/s2)t2
4.90t2 – 5.14t – 2.34 = 0
t = {5.14 ± [(5.14)2 – 4(4.90)(–2.34)]1/2}/(9.80)
t = 1.39 s
Problem#2
A block of mass M rests on a table. It is fastened to the lower end of a light vertical spring. The upper end of the spring is fastened to a block of mass m. The upper block is pushed down by an additional force 3mg, so the spring compression is 4mg/k. In this configuration the upper block is released from rest. The spring lifts the lower block off the table. In terms of m, what is the greatest possible value for M?
Answer:
If the spring is just barely able to lift the lower block from the table, the spring lifts it through no
noticeable distance, but exerts on the block a force equal to its weight Mg. The extension of the
spring, from Fs = │kx│, must be Mg/k. Between an initial point at release and a final point when the
moving block first comes to rest, we have
∆Emech = ∆K + ∆U
0 = Kf – Ki + Ugf – Ugi + Usf – Usi
0 = 0 – 0 + mg(Mg/k) – mg(–4mg/k) + ½ k(Mg/k)2 – ½k(–4mg/k)
8m2g2/k – 4m2g2/k = mMg2/k + M2g2/2k
4m2 = mM + M2/2
½M2 + mM – 4m2 = 0
M = {–m ± [m2 – 4(½)(–4m2)]1/2} = –m ± 3m
Only a positive mass is physical, so we take M = 2m
Problem#3
A ball having mass m is connected by a strong string of length L to a pivot point and held in place in a vertical position. A wind exerting constant force of magnitude F is blowing from left to right as in Figure 2a. (a) If the ball is released from rest, show that the maximum height H reached by the ball, as measured from its initial height, is
Check that the above result is valid both for cases when 0 ≤ H ≤ L and for L ≤ H ≤ 2L. (b) Compute the value of H using the values m = 2.00 kg, L = 2.00 m, and F = 14.7 N. (c) Using these same values, determine the equilibrium height of the ball. (d) Could the equilibrium height ever be larger than L? Explain.
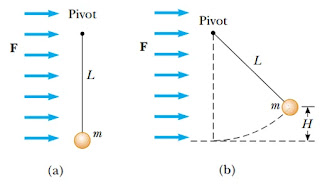 |
| Fig.2 |
Answer:
(a) Take the original point where the ball is released and the final point where its upward swing stops at height H and horizontal displacement
x2 = L2 + (L – H)2
x = [2LH – H2]1/2
Since the wind force is purely horizontal, it does work
Wwind = ∫F.ds
Wwind = F∫dx
Wwind = F[2LH – H2]1/2
The work-energy theorem can be written:
∆Emech = ∆K + ∆U
Wwind = Kf – Ki + Uf – Ui
Wwind = 0 – 0 + mgH – 0
F[2LH – H2]1/2 = mgH, or
2F2LH – F2H2 = m2g2H2
2F2L = (F2 + m2g2)H
H = 2F2L/(F2 + m2g2) or
H = 2L/[1 + (mg/F)2]
As F → 0 , H → 0 as is reasonable.
As F → ∞ , H → 2L , which would be hard to approach experimentally
(b) the value of H using the values m = 2.00 kg, L = 2.00 m, and F = 14.7 N is
H = 2(2.00 m)/{1 + [2.00 kg)(9.80 m/s2)/14.7 N]2}
H = 1.44 m
(c) Call φ the equilibrium angle with the vertical.
∑Fx = 0
T sinφ = F (*)and
∑Fy = 0
T cosφ = mg (**)
From (*) and (**), we get
tanφ = F/mg = (14.7 N)/[(2.00 kg)(9.80 m/s2)] = 0.750
φ = tan-1(0.750) = 36.90
Therefore,
Heq = L(1 – cosφ) = (2.00 m)(1 – cos36.90) = 0.400 m
(d) As F → ∞ , tanθ → ∞ , θ → 90.00 and Heq → L
A very strong wind pulls the string out horizontal, parallel to the ground. Thus,
(Heq)max = L
Post a Comment for "Potential Energy Additional Problems and Solutions 6"