Problem#1
A roller-coaster car is released from rest at the top of the first rise and then moves freely with negligible friction. The roller coaster shown in Figure 1 has a circular loop of radius R in a vertical plane. (a) Suppose first that the car barely makes it around the loop: at the top of the loop the riders are upside down and feel weightless. Find the required height of the release point above the bottom of the loop in terms of R. (b) Now assume that the release point is at or above the minimum required height. Show that the normal force on the car at the bottom of the loop exceeds the normal force at the top of the loop by six times the weight of the car. The normal force on each rider follows the same rule. Such a large normal force is dangerous and very uncomfortable for the riders. Roller coasters are therefore not built with circular loops in vertical planes. Figure P6.20 and the photograph on page 157 show two actual designs.
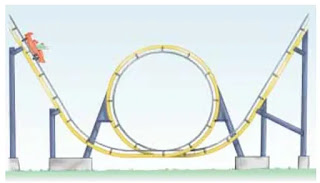 |
| Fig.1 |
Answer:
(a) At the top of the loop the car and riders are in free fall (nC = 0):
∑Fy = mv2/R
nC + mg = mv2/R
v = √(gR)
Energy of the car-riders-Earth system is conserved between release and top of loop (A to C):
KA + UgA = KC + UgC
0 + mgh = ½ mv2 + mg(2R)
gh = ½ gR + 2gR
h = 2.50R
(b) Let h now represent the height ≥ 2.50R of the release point. At the bottom of the loop we have
KA + UgA = KB + UgB
0 + mgh = ½ mvB2 + 0
VB = √(2gh)
at B:
∑Fy = mvB2/R
nB – mg = m(2gh)/R
nB = mg + 2mgh/R (*)
At the top of the loop (A to C),
KA + UgA = KC + UgC
0 + mgh = ½ mvC2 + mg(2R)
vC2 = 2gh – 4gR, and
at C:
∑Fy = mv2/R
nC + mg = mvC2/R
nC + mg = m[2gh – 4gR]/R
nC = 2mgh/R – 5mg (**)
from (*) and (**) we get the normal force at the bottom is larger by
nB – nC = mg + 2mgh/R + 5mg – 2mgh/R
nB – nC = 6mg
Problem#2
Review problem. In 1887 in Bridgeport, Connecticut, C. J. Belknap built the water slide shown in Figure 4. A rider on a small sled, of total mass 80.0 kg, pushed off to start at the top of the slide (point A) with a speed of 2.50 m/s. The chute was 9.76 m high at the top, 54.3 m long, and 0.51 m wide. Along its length, 725 wheels made friction negligible. Upon leaving the chute horizontally at its bottom end (point C), the rider skimmed across the water of Long Island Sound for as much as 50 m, “skipping along like a flat pebble,” before at last coming to rest and swimming ashore, pulling his sled after him. According to Scientific American, “The facial expression of novices taking their first adventurous slide is quite remarkable, and the sensations felt are correspondingly novel and peculiar.” (a) Find the speed of the sled and rider at point C. (b) Model the force of water friction as a constant retarding force acting on a particle. Find the work done by water friction in stopping the sled and rider. (c) Find the magnitude of the force the water exerts on the sled. (d) Find the magnitude of the force the chute exerts on the sled at point B. (e) At point C the chute is horizontal but curving in the vertical plane. Assume its radius of curvature is 20.0 m. Find the force the chute exerts on the sled at point C.
 |
| Fig.4 |
Answer:
(a) Conservation of energy for the sled-rider-Earth system, between A and C:
KA + UgA = KC + UgC
½ m(2.50 m/s)2 + m(9.80 m/s2)(9.76 m) = ½ mvC2
vC2 = 198
vC = 14.1 m/s
 |
| Fig.5 |
(b) Incorporating the loss of mechanical energy during the portion of the motion in the water, we have, for the entire motion between A and D (the rider’s stopping point),
∆Emech = ∆K + ∆U
∆Emech = KD – KA + UgD – UgA
∆Emech = 0 – ½ (80.0 kg)(2.50 m/s)2 + 0 – (80.0 kg)(9.80 m/s2)(9.76 m)
∆Emech = –7.90 kJ
(c) The water exerts a frictional force is
∆Emech = –fk∆x = –7.90 kJ
fk = 7.90 kJ/50 m = 158 N
and also a normal force of n = mg = (80 kg)(9.80 m/s2) = 784 N, then
The magnitude of the water force is
Fwater = [(784 N)2 + (158 N)2]1/2 = 800 N
(d) The angle of the slide is
sinθ = (9.76 m)/(54.3 m) = 0.1797
θ = 10.40
For forces perpendicular to the track at B,
nB = mgsinθ = (80.0 kg)(9.80 m/s2)sin10.40 = 771 N
(e) the force the chute exerts on the sled at point C, given by
∑Fy = mvC2/R
nC – mg = mvC2/R
nC = (80.0 kg)[(9.80 m/s2) – (14.1 m/s)2/20 m] = 1.57 kN (up)
The rider pays for the thrills of a giddy height at A, and a high speed and tremendous splash at C. As a bonus, he gets the quick change in direction and magnitude among the forces we found in parts (d), (e), and (c).


Post a Comment for "Potential Energy Additional Problems and Solutions 8"