Q#1
A vector is not changed if(a) It is rotated through an arbitrary angle
(b) It is multiplied by an arbitrary scalar
(c) It is cross-multiplied by a unit vector
(d) It is slid parallel to itself
Answer: (d)
(d) is correct because if it is slid parallel to itself that does not change the direction or magnitude of the vector. In the case of (a) and (c) the direction of the vector changes while in the case of (b) magnitude of the vector changes.
Q#2
Which of the sets given below may represent the magnitudes of three vectors adding to zero?
(a) 2, 4, 8 (b) 4, 8, 16 (c) 1, 2, 1 (d) 0.5, 1, 2
Answer: (c)
(c) is correct answer because if the sum of three vectors is zero then their magnitudes represent a triangle and one of the properties of triangles is that sum of any two sides is greater than the third side. Options (a),(b) and (d) do not follow this condition so they can not form a triangle. In option (c) 1 + 1 = 2, so it is a special case of a triangle of which all three sides are collinear. See also the figure below:
(i) If three vectors add to zero their magnitudes represent three sides of a triangle. Sum of any two sides of triangle is greater than the third.
(ii) In special if sum of two sides is equal to the third then all the three sides of the triangle are along the same line ie they are collinear. Angle of this triangle are 0, and 1800. Figure (ii) makes it clear.
Q#3
Resultant of A and B makes an angle α with A and β with B,
(a) α < β
(b) α < β if A < B
(c) α < β if A >B
(d) α < β if A = B
Answer: (c)
It will be clear from parallelogram law of addition of two vectors that the resultant makes a smaller angle with the greater vector.
(ii) In special if sum of two sides is equal to the third then all the three sides of the triangle are along the same line ie they are collinear. Angle of this triangle are 0, and 1800. Figure (ii) makes it clear.
Resultant of A and B makes an angle α with A and β with B,
(a) α < β
(b) α < β if A < B
(c) α < β if A >B
(d) α < β if A = B
Answer: (c)
It will be clear from parallelogram law of addition of two vectors that the resultant makes a smaller angle with the greater vector.
For Figure: OA = magnitude of vector A, OB = magnitude of vector B, OC = magnitude of resultant vector, α and β are angles between reslutant vector and vectors A and B respectively. It is clear from above diagram that as vector A increases α decreases. When A > B, α < β.
Q#4
The component of a vector is
(a) Always less than its magnitude
(b) Always greater than its magnitude
(c) Always equal to its magnitude
(d) None of these
Answer: (d)
The component of a vector may be less than, greater than or equal to its magnitude. It will be clear from the following figure.
The component of a vector is
(a) Always less than its magnitude
(b) Always greater than its magnitude
(c) Always equal to its magnitude
(d) None of these
Answer: (d)
The component of a vector may be less than, greater than or equal to its magnitude. It will be clear from the following figure.
OA’ is one of the components of vector OA. Below is the three conditions when magnitude of component OA’ is equal to, less than or greater than magnitude of vector OA.
Q#5
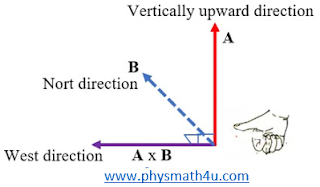
A vector A points vertically upward and B points towards the north. The vector product A x B.
(a) along west
(b) along east
(c) zero
(d) vertically downward.
Answer: (a)
The cross product A x B is a vector, direction of which will be perpendicular to the plane of A and B. Given the condition this direction may be along west or east. Using the right-hand rule it can be found that this is west.
Q#5
A vector A points vertically upward and B points towards the north. The vector product A x B.
(a) along west
(b) along east
(c) zero
(d) vertically downward.
Answer: (a)
The cross product A x B is a vector, direction of which will be perpendicular to the plane of A and B. Given the condition this direction may be along west or east. Using the right-hand rule it can be found that this is west.
The direction of thumb gives direction of cross product of vectors A x B.
Q#6
The radius of a circle is stated as 2.12 cm. Its area should be written as
(a) 14 cm²
(b) 14.1 cm²
(c) 14.11 cm²
(d) 14.1124 cm²
Answer: (b)
The area of circle A = π.r²
π = 3.14, r = 2.12 cm. The minimum number of significant digits in this multiplication quantities is three, hence the result should also have three significant digits rounded.
Q#6
The radius of a circle is stated as 2.12 cm. Its area should be written as
(a) 14 cm²
(b) 14.1 cm²
(c) 14.11 cm²
(d) 14.1124 cm²
Answer: (b)
The area of circle A = π.r²
π = 3.14, r = 2.12 cm. The minimum number of significant digits in this multiplication quantities is three, hence the result should also have three significant digits rounded.
A = 3.141 x 2.12 x 2.12 cm² = 14.1124 cm² =14.1 cm²
Third significant digit is 1 which is to be rounded. Next to it is 1 which is less than 5.
So, the fourth digit onwards will be dropped and 14.1124 cm² rounded to three significant digits is 14.1 cm².



Post a Comment for "Questions OBJECTIVE - I and Answer (Physics and Mathematics) HC Verma Part 1"