Q#1
Consider the motion of the tip of the minute hand of a clock. In one hour (a) the displacement is zero(b) the distance covered is zero(c) the average speed is zero
(d) the average velocity is zero.
Answer: (a), (d)
In one hour the tip of the minute hand comes to the same position, so its displacement and average velocity are zero. Hence (a) and (d) is correct. But in this time the tip covers a distance equal to the circumference of a circle of radius equal to the length of the minute hand. So (b) and (c) are incorrect.
Q#2
A particle moves along the X-axis as
X = u(t – 2s) + a(t – 2s)² .
(a) the initial velocity of the particle is u
(b) the acceleration of the particle is a
(c) the acceleration of the particle is 2a
(d) at t = 2 s particle is at the origin.
Answer: (c), (d)
The velocity at any instant is given by v = dx/dt = u + 2a(t – 2)
initial velocity is the velocity at t = 0, putting this value we get v = u – 4a which is not zero. So (a) is incorrect.
Acceleration is given by dv/dt = 2a, So (b) is incorrect and (c) is correct.
Putting t = 2 s in the given displacement equation we get x = 0, so (d) is also correct.
Q#3
Pick the correct statement:
(a) The average speed of a particle in a given time is never less than the magnitude of the average velocity
(b) It is possible to have a situation in which |dv/dt| ≠ 0 but d|v|/dt=0
(c) The average velocity of a particle is zero in a time interval. It is possible that the instantaneous velocity is never zero in the interval.
(d) The average velocity of a particle moving on a straight line is zero in a time interval. It is possible that the instantaneous velocity is never zero in the interval. (Infinite accelerations are not allowed.)
Answer: (a), (b), (c)
Since the distance covered by a particle in a given time will never be less than the magnitude of displacement, so the average speed is never less than the magnitude of the average velocity. (a) is correct.
|dv/dt| is the magnitude of the acceleration and d|v|/dt is the rate of change of speed. Consider the case of uniform circular motion. Here speed of the particle is constant, so d|v|/dt = 0. But magnitude of the acceleration |dv/dt| ≠ 0. (b) is also correct.
As we have seen in question no 1, the average velocity of the tip of the minute hand is zero in the time interval of one hour, but its instantaneous velocity is never zero in this interval. So (c) is also correct.
If the average velocity of a particle moving on a straight line is zero in a time interval, it means its displacement is zero. It can only be possible if the particle has returned back to its original position at least once in this time interval. So at the instant when it reverses the direction of its velocity, the instantaneous velocity of the particle will definitely be zero. So (d) is incorrect.
Q#4
An object may have
(a) varying speed without having varying velocity
(b) varying velocity without having varying speed
(c) nonzero acceleration without having varying velocity
(d) nonzero acceleration without having varying speed
Answer: (b), (d)
If the velocity is constant, speed can not vary. So (a) is not true.
In a uniform circular motion velocity varies while speed remains constant and since the velocity varies acceleration is non zero. So (b) and (d) both are true.
The rate of change of velocity is acceleration, so without having varying velocity, the acceleration is zero. So (c) is not true.
Q#5
Mark the correct statements for a particle going on a straight line:
(a) If the velocity and acceleration have opposite sign, the object is slowing down.
(b) If the position and velocity have opposite sign, the particle is moving towards the origin.
(c) If the velocity is zero at an instant, the acceleration should also be zero at that instant.
(d) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.
Answer: (a), (b), (d)
If the acceleration and velocity of the particle have opposite signs, it has a retarding effect. As is the case of a particle thrown vertically upward. So (a) is true. (b) is also obviously true.
(c) is not true. Consider the case of a particle thrown vertically upward. At its highest point, the velocity is zero but acceleration is not zero.
Acceleration is defined as the rate of change of velocity. If in a time interval velocity is zero, it means in this interval velocity does not change. So acceleration at any instant in this time interval is zero. Hence (d) is true.
Q#6
The velocity of a particle is zero at t = 0.
(a) The acceleration at t = 0 must be zero.
(b) The acceleration at t = 0 may be zero
(c) If the acceleration is zero from t = 0 to t =10 s, the speed is also zero in this interval.
(d) If the speed is zero from t = 0 to t =10 s, the acceleration is also zero in this interval.
Answer: (b), (c), (d)
(a) is not true. Consider the case of a particle dropped vertically downward, its velocity at t = 0 is zero but acceleration is not zero.
(b) is true because we do not have information about the velocity in next instants. If in next instants the velocity still remains zero, the acceleration will be zero.
(c) is true because, if acceleration is zero that means there is no change in velocity. The velocity remains zero in this interval.
(d) is true because if the speed remains zero from t = 0 to t = 10 s, that means the particle is at rest in this interval, so the acceleration is also zero in this interval.
Q#7
Mark the correct statements :
(a) The magnitude of the velocity of a particle is equal to its speed.
(b) The magnitude of average velocity in an interval is equal to its average speed in that interval.
(c) It is possible to have a situation in which the speed of a particle is always zero but the average speed is not zero.
(d) It is possible to have a situation in which the speed of the particle is never zero but the average speed in an interval is zero.
Answer: (a).
At any instant, the magnitude of the velocity is also its speed. So (a) is correct.
(b) is incorrect because velocity is displacement in unit time while speed is distance covered in unit time.
(c) is incorrect because if speed is zero in a time interval, that means the particle has not moved in this interval and no distance traveled. So average speed has to be zero.
(d) is incorrect because if the speed of the particle is never zero, means it has traveled some distance. So, the average speed in the interval will not be zero.
Q#8
The velocity-time plot for a particle moving on a straight line is shown in the figure (3-Q4).
(a) The particle has a constant acceleration.
(b) The particle has never turned around.
(c) The particle has zero displacements.
(d) The average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20 s.
Answer: (a), (d).
(a) is true because in a velocity-time graph the slope (which shows the rate of change of velocity) denotes acceleration. In this graph the slope is constant, so acceleration is constant.
(b) is not true because at t = 10 s the velocity changes its sign from positive to negative, means it has turned around.
(c) is not true because displacement in the positive direction of v is given by the area of the graph above the time axis and displacement in the negative direction of v is given by the area of the graph below the time axis. In this case, later is greater than former not equal. So, displacement is not zero.
(d) is true because in 0 to 10 s speed changes from 10 to 0 m/s and in 10 to 20 s speed changes from 0 to 10 m/s. So average speed will be the same.
Q#9
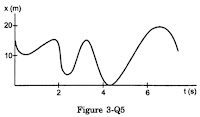
Figure (3-Q5) shows the position of a particle moving on the X-axis as a function of time.
(a) The particle has come to rest 6 times.
(b) The maximum speed is at t = 6 s.
(c) The velocity remains positive for t = 0 to t = 6 s.
(d) The average velocity for the total period shown is negative.
Answer: (a).
Slope of the curve at any point gives the velocity of the particle at that point. In the given graph the curve has three troughs and three crests. At these points, the slope of the curve (tangent is horizontal to time axis) is zero. So, at six points velocity is zero, means it has come to rest.
(b) is not true because the slope of the curve is not maximum at t = 6 s.
(c) is not true because the gradient of the slope is not positive always between t = 0 to t = 6 s.
(d) is not true because the final displacement is not less than the initial.
Q#10
The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/S².
(a) The frame must be at rest with respect to each other.
(b) The frames may be moving with respect to each other but neither should be accelerated with respect to the other.
(c) The acceleration of S2 with respect to S1 may either be zero or 8 m/s².
(d) The acceleration of S2 with respect to S1 may be anything between 0 and 8 m/s²
Answer: (d).
The acceleration of S2 with respect to S1 is given by
a = ap,s1 - ap,s2, This vector sum can be easily understood by the following figure:
Magnitude of both aps1 and aps2 = 4 m/s2
Depending upon angle OPO’ (from 00 to 1800) magnitude of a may be anything between zero and 8 m/s2


Post a Comment for "Questions OBJECTIVE - II and Answer (Rest and Motion: Kinematics) HC Verma Part 1"