Q#12
If the tension in the string in figure (6-E3) is 16 N and the acceleration of each block is 0.5 m/s², Find the friction coefficients at the two contacts with the blocks.
Answer:
Friction force on the 2 kg block is µN = µ1(2g) and it will act opposite to tension force of 16 N applied by the string. Since acceleration is 0.5 m/s², the force-acceleration equation is
F = ma
16 – µ1(2g) = 2(0.5)
µ1(2g) = 15
µ1 = 0.75 (Taking g = 10 m/s²)
So, friction coefficient at 2 kg block is µ1 = 0.75
Let us consider the 4 kg block, Normal force on the block
= mg cosθ = 4g cos30° = 4 x 10 x (√3/2) (Taking g = 10 m/s²)
= 20√3 N
Friction force on the block = µ2(20√3) N
Net force on the block along the plane = 4g sinθ – 16 – µ2(20√3)
From the force-acceleration equation,
4g sinθ – 16 – µ2(20√3) = 4 x 0.5
40sin30° – µ2(20√3) = 18
µ2 ≈ 0.06
So, friction coefficient at 4 kg block is µ2 = 0.06
Q#13
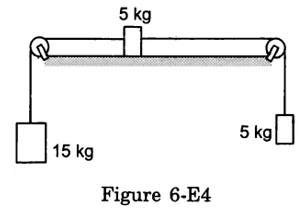
The friction coefficient between the table and the block shown in figure (6-E4) is 0.2, find the tensions in the two strings.
= mg cosθ = 4g cos30° = 4 x 10 x (√3/2) (Taking g = 10 m/s²)
= 20√3 N
Friction force on the block = µ2(20√3) N
Net force on the block along the plane = 4g sinθ – 16 – µ2(20√3)
From the force-acceleration equation,
4g sinθ – 16 – µ2(20√3) = 4 x 0.5
40sin30° – µ2(20√3) = 18
µ2 ≈ 0.06
So, friction coefficient at 4 kg block is µ2 = 0.06
Q#13
The friction coefficient between the table and the block shown in figure (6-E4) is 0.2, find the tensions in the two strings.
Answer:
Let the tension in the string connected to 15 kg block be T and to the 5 kg block be T'. If accelerations of block and weights be 'a' then applying force-acceleration equation (Derived from Newton's second Law of Motions) we get,
15g – T = 15a
T = 15g – 15a
and T' – 5g = 5a
T' = 5g + 5a
for block,
T – T' - µ(5g) = 5a
T – T' = 0.2(5g) + 5a
15g – 15a – 5g – 5a = g + 5a
25a = 9g
a = 18/5 m/s² (Taking g =10 m/s²)
From (i),
T= 15 x 10 – 15(18/5) = 150 – 54 = 96 N
So, tension in the left string = 96 N
From (ii),
T' = 5 x 10 + 5(18/5) = 68 N
So, tension in the right string = 68 N
Q#14
The friction coefficient between a road and the Tyre of a vehicle is 4/3. Find the maximum incline the road may have so that once hard brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5 m.
Answer:
Let us first find the retardation of the vehicle from the given data. Initial velocity u = 36 km/hr = 36000/3600 m/s =10 m/s, Final velocity v= 0, Distance traveled s = 5 m, if retardation is 'a',
v² = u² – 2as
0 = 100 – 2a(5)
a = 10 m/s²
Let the angle of inclination be θ and the mass of the vehicle be m. Normal force on the vehicle = mgcosθ
Friction force = µN = (4/3)mgcosθ
Net force along the incline against the motion
= (4/3)mgcosθ – mgsinθ
Using force-acceleration relationship we get,
(4/3)mgcosθ – mgsinθ = ma = m(10) = 10m
4gcosθ – 3gsinθ = 30
3 sinθ – 4 cosθ + 3 = 0
3(1 + sinθ) = 4 cosθ
(1 + sinθ)/cosθ = 4/3
(cos ½θ + sin ½θ)/(cos ½θ – sin ½θ) = 4/3
(1 + tan ½θ)/(1 – tan ½θ) = 4/3
3 + 3 tan ½θ = 4 – 4 tan ½θ
7 tan ½θ = 1
tan ½θ = 1/7
θ = 16°
So, the maximum incline will be 16°.
Q#15
The friction coefficient between an athlete's shoes and the ground is 0.90. Suppose a superman wears these shoes and and races for 50 m. There is no upper limit on his capacity of running at high speeds. (a) Find the minimum time he will have to take in completing the 50 m starting from rest. (b) Suppose he takes exactly this minimum time to complete the 50 m, what minimum time will he take to stop.
Answer:
(a) Given µ = 0.90, if mass of superman = m, then maximum force of friction between shoes and ground = µmg. He can not apply more force on the ground to increase the speed because then the shoes will slip. If the acceleration of the superman be 'a', then,
a = force/mass = µmg/m = µg = 9 m/s².
Now initial velocity u = 0, Distance s = 50 m, a = 9 m/s², time t =?
from, s = ut + ½at²
50 = 0 + ½(9)t²
t² = 100/9
t = 3.3 s
So, the minimum time he will have to take in completing the 50 m starting from rest = 3.3 s
(b) To stop he will have to depend on maximum friction force that will be again µmg and the retardation = µmg/m = µg = 0.9 x 10 = 9 m/s². Speed of superman at completing
50 m = u + at = 0 + 9(10)/3 = 30 m/s
Now this is the initial speed during the stopping
So, u = 30m/s, v = 0 m/s, a = –9 m/s²
from v = u + at
0 = 30 – 9t
t = 30/9 s = 3.3 s
So, he will take exactly the same time to stop = 3.3 s.
Q#16
A car is going at a speed of 21.6 km/hr when it encounters a 12.8 m long slope of angle 30° (figure 6-E5). The friction coefficient between the road and the tyre is ½√3. Show that no matter how hard the driver applies the brakes, the car will reach the bottom with a speed greater than 36 km/hr. Take g = 10 m/s².
Answer:
Let mass of the car be m, Normal force on the car by the incline
= mgcos30° = ½mg√3
Maximum friction force = ½ µmg√3 = mg/4
Component of weight along slope = mgsin30° = mg/2
Net force down the incline = ½ mg – ¼mg = ¼mg
Acceleration = Force/mass = mg/4m= g/4 = 2.5 m/s²
Now Initial velocity u = 21.6 km/hr = 21.6(1000/3600) m/s = 6 m/s, Distance s = 12.8 m, a = 2.5 m/s², final velocity v = ?
from v² = u² + 2as
v² = 6² + 2(2.5)12.8 =100
v = 10 m/s = 36 km/hr
It is the minimum speed that the car can have at the bottom of the slope.
So, no matter how hard the driver applies the brakes, the car will reach the bottom with a speed greater than 36 km/hr.




Post a Comment for "Solutions to Exercises on Friction HC Verma's Concepts of Physics Part 1 (12-16)"