Q#22
A 2 kg block is placed over a 4 kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.20. Find the acceleration of two blocks if a horizontal force of 12 N is applied to (a) the upper block, (b) the lower block. Take g = 10 m/s².Answer:
(a) When the force of 12 N is applied to the upper 2 kg block, See the forces on the blocks in the diagrams below:
Consider the upper block as in figure-1 above.
Weight of 2 kg block = 2g = 20 N = R, Normal force on the block by the lower block. Given µ = 0.20,
Force of friction = µR = 0.20(20)N = 4 N
This force of friction will act against the motion which is in the direction of 12 N force. So net force on the block = 12 – 4 N = 8 N
If acceleration of this block be 'a' then
a = Force/mass = 8 N/2 kg = 4 m/s²
Consider the lower block as in figure-2 above.
Since the block is placed on a smooth surface so friction force from the lower surface is zero. But the friction force by the upper block surface on it will be same as the friction force applied by the lower block on the upper block but opposite in direction according to the Newton's Third Law.
So, the friction force 4 N will be along the 12 N force. Only force in the horizontal direction for the lower block is this 4 N which will induce acceleration to it. Let the acceleration be a'.
a' = Force/mass = 4 N/4 kg = 1 m/s².
(b) When the force of 12 N is applied to the lower 4 kg block, See the forces on the blocks in the diagrams below:
Weight of 2 kg block = 2g = 20 N = R, Normal force on the block by the lower block. Given µ = 0.20,
Force of friction = µR = 0.20(20)N = 4 N
This force of friction will act against the motion which is in the direction of 12 N force. So net force on the block = 12 – 4 N = 8 N
If acceleration of this block be 'a' then
a = Force/mass = 8 N/2 kg = 4 m/s²
Consider the lower block as in figure-2 above.
Since the block is placed on a smooth surface so friction force from the lower surface is zero. But the friction force by the upper block surface on it will be same as the friction force applied by the lower block on the upper block but opposite in direction according to the Newton's Third Law.
So, the friction force 4 N will be along the 12 N force. Only force in the horizontal direction for the lower block is this 4 N which will induce acceleration to it. Let the acceleration be a'.
a' = Force/mass = 4 N/4 kg = 1 m/s².
(b) When the force of 12 N is applied to the lower 4 kg block, See the forces on the blocks in the diagrams below:
Consider the lower block as in figure-3 above.
Lower surface is smooth so no friction force by the lower surface but for the upper surface the weight of 2g N of upper block is normal force so friction force at this surface = µ(2g) = 0.20(2)(10)
= 4 N and its direction will be opposite to 12 N applied force.
So acceleration of lower block = a' = Force/mass
= (12 – 4)N/4 kg = 8 N/4 kg = 2 m/s²
Consider the upper block as in figure-4 above.
The weight of 2g N is balanced by the normal force of equal and opposite magnitude. There is no applied force on it but the force of friction applied to the lower block will have equal and opposite reaction, so the friction force of 4 N will act in the direction of 12 N force and this 4 N force of friction is the only horizontal force on the upper block that will induce acceleration to it.
So, the acceleration of upper block a = 4 N/2 kg = 2 m/ s².
Q#23
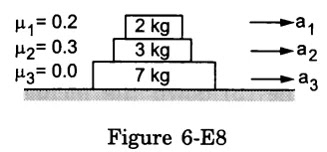
Find the accelerations a1, a2, a3of the three blocks shown in figure (6-E8). If a horizontal force of 10N is applied on (a) 2 kg block (b) 3 kg block, (c) 7 kg block. Take g = 10 m/s².
Lower surface is smooth so no friction force by the lower surface but for the upper surface the weight of 2g N of upper block is normal force so friction force at this surface = µ(2g) = 0.20(2)(10)
= 4 N and its direction will be opposite to 12 N applied force.
So acceleration of lower block = a' = Force/mass
= (12 – 4)N/4 kg = 8 N/4 kg = 2 m/s²
Consider the upper block as in figure-4 above.
The weight of 2g N is balanced by the normal force of equal and opposite magnitude. There is no applied force on it but the force of friction applied to the lower block will have equal and opposite reaction, so the friction force of 4 N will act in the direction of 12 N force and this 4 N force of friction is the only horizontal force on the upper block that will induce acceleration to it.
So, the acceleration of upper block a = 4 N/2 kg = 2 m/ s².
Q#23
Find the accelerations a1, a2, a3of the three blocks shown in figure (6-E8). If a horizontal force of 10N is applied on (a) 2 kg block (b) 3 kg block, (c) 7 kg block. Take g = 10 m/s².
Answer:
(a) When a horizontal force of 10 N is applied to 2 kg block
Normal force on 2 kg block = weight of 2 kg block = 2g N = 20 N
Friction force on 2 kg block = µ1(20 N) = 0.2 x 20 N = 4 N
Net horizontal force on 2 kg block = 10 – 4 = 6 N
Acceleration a1 = 6 N/2 kg = 3 m/s²
3 kg block
Upper surface of this block will have friction force same as above but opposite in direction i.e. 4 N along applied force of 10 N.
Normal force on the lower surface = Total weight of both blocks = 5g = 50 N
Friction force = µ2(50) = 0.3(50) = 15 N but it can not be more than the 4 N. It means that the 3 kg and 7 kg blocks do not move with respect to each other.
To calculate the acceleration of these blocks we consider both as if attached. Total mass = 3 kg +7 kg = 10 kg. Total downward force on the smooth surface due to weights
= 10g + 2g = 12g = 120 N = Normal force on the lower surface of 7 kg block.
Friction force on this surface = µ3(120) = (0)(120) = 0
Now the net external force on this combined block is the friction force applied by the top most block = 4 N.
Acceleration of combined block = Force/mass
= 4 N/10 kg = 0.40 m/s²
Hence a2=a3 = 0.40 m/s²
(b) When a horizontal force of 10 N is applied to 3 kg block
Friction forces opposing the movement are on both surfaces of the 3 kg block. Normal force on upper surface = 2g N
Limiting Friction force on upper surface = µ1(2g) = 0.2(2)10 = 4 N
Normal force on the lower surface = 2g + 3g = 50 N
Friction force on lower surface = µ2(5g) = 0.3 x 50 = 15 N but it is the limiting value ; in this case it can not be more than applied force of 10 N meaning thereby that the lower two blocks do not move with respect to each other but move combined on the lower most surface.
So, consider the lower two blocks combined. As far as upper 2 kg block is concerned we do not know whether the limiting value of friction force 4 N is attained or not.
So, let us proceed with assumption that it is attained, then,
Mass of combined block = 7 kg +3 kg = 10 kg
Total normal force on the block by the lower most surface = (2 +10)g = 120 N
Friction force on the block = µ3(120) = (0)(120) = 0
So net horizontal force on this combined block = 10 N – 4 N =6 N
Acceleration of this combined block = 6 N/10 kg = 0.6 m/s²
on 2 kg Block
Only horizontal force on this block is friction force = 4 N
Acceleration of 2 kg upper block a1 = 4 N/2 kg = 2 m/s² which is greater than the acceleration of lower combined blocks 0.6 m/s² that is not possible. So our assumption that limiting friction force of 4 N is attained between 2 kg and 3 kg blocks is not true. Since this friction force is less than limiting, it means that 2 kg block do not move with respect to 3 kg block as a result all the three blocks move combined. Total mass of three combined blocks = 12 kg, Force applied = 10 N,
Hence acceleration = 10 N/12 kg = 5/6 m/s²
So a1 = a2 = a3 = 5/6 m/s²
(c) When a horizontal force of 10 N is applied to 7 kg block
Since the friction coefficient on lower most surface = µ3 = 0, means there is no friction force on the lower surface of the 7 kg block. On the upper surface of the 7 kg block normal force = 5g N
Limiting Friction force = µ2(5g) = 0.30 x 50 N = 15 N but it can not be more than the applied force, so there is no relative movement between 3 kg and 7 kg block and they move combined. Normal force on the upper surface of 3 kg block = 2g N = 20 N
Limiting Friction force at this surface = µ1(20) = 0.2 x 20 N = 4 N
Same as in the above case (b) we can prove that this limiting friction force is not achieved and thus even the 2 kg block move together with the 3 kg and 7 kg block.
Similarly, combined acceleration of the three blocks = Total external force/total mass = 10N/12kg = 5/6 m/s²
Hence accelerations a1 = a2 = a3 = 5/6 m/s²
Q#24
The friction coefficient between the two blocks shown in figure(6-E9) is µ but the floor is smooth (a) what maximum horizontal force F can be applied without disturbing the equilibrium of the system? (b) suppose the horizontal force applied is double of that found in part(a), find the acceleration of the two masses.
Answer:
(a)At maximum F friction force between the two blocks will be limiting = f = µN, where N is normal force.
Since N = mg, f = µmg, its direction will be opposite to F on block 'm'.
Let the tension in the string around the pulley be T, See the Free body diagram of upper block below, Figure -1,
Since the block is in equilibrium, sum of horizontal forces = 0,
i.e. F – f – T = 0
F = f + T
Consider the lower block. Friction force by the upper block = f = µmg but opposite in direction that of on upper block. Lower surface is smooth, so no friction force by it. Normal force by the surface = (M + m)g. Horizontal force by string = T as shown in the Free body diagram Figure-2. At equilibrium sum of all horizontal forces are zero,
i.e. T – f = 0
T = f = µmg
Putting this value in (a)
F = f + T = 2f = 2µmg
(b) When the force applied is doubled, F = 4µmg, limiting friction is crossed and there is net horizontal force causing acceleration. In this case accelerations of the two blocks 'a' are equal.
So for the upper block, F – f – T = ma
And for the lower block, T – f = Ma
T = f + Ma
Putting this in (b)
F – f – f – Ma = ma
(M + m)a = F – 2f = 4µmg – 2µmg = 2µmg
a = 2µmg/(M + m)
Q#25
Suppose the entire system of the previous question is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
i.e. F – f – T = 0
F = f + T
Consider the lower block. Friction force by the upper block = f = µmg but opposite in direction that of on upper block. Lower surface is smooth, so no friction force by it. Normal force by the surface = (M + m)g. Horizontal force by string = T as shown in the Free body diagram Figure-2. At equilibrium sum of all horizontal forces are zero,
i.e. T – f = 0
T = f = µmg
Putting this value in (a)
F = f + T = 2f = 2µmg
(b) When the force applied is doubled, F = 4µmg, limiting friction is crossed and there is net horizontal force causing acceleration. In this case accelerations of the two blocks 'a' are equal.
So for the upper block, F – f – T = ma
And for the lower block, T – f = Ma
T = f + Ma
Putting this in (b)
F – f – f – Ma = ma
(M + m)a = F – 2f = 4µmg – 2µmg = 2µmg
a = 2µmg/(M + m)
Q#25
Suppose the entire system of the previous question is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
Answer:
Since the elevator is coming down with an acceleration 'a' the weights of the blocks will reduce to m(g - a) and M(g - a) and accordingly the Normal forces will change. So we can follow the same process as in problem number 24, and get answers with just a replacement of 'g' by 'g - a' as follows:
(a) F = f + T = 2f = 2µm(g – a)
(b) a = 2µm(g – a)/(M + m)
Q#26
Consider the situation shown in the figure (6-E9). Suppose a small electric field E exists in the space in the vertically upward direction and the upper block carries a positive charge Q on its top surface. The friction coefficient between the two blocks is µ but the floor is smooth. What maximum horizontal force F can be applied without disturbing the equilibrium?
[Hint: The force on a charge Q by the electric field E is F = QE in the direction of E.]
Answer:
an additional force = QE in the upper direction on the upper block is applied due to electric field E, see the figures below,
N + QE = mg
N = mg – QE
Friction force on upper block, f = µN = µ(mg – QE)
For the equilibrium in the horizontal direction F = T + f (i)
Consider the equilibrium of lower block in vertical direction,
N’ = Mg + mg – QE
since the surface is smooth there is no friction on the lower surface of lower block, but the upper surface of the lower block will have friction force P by the upper block in the opposite direction.
So, for the equilibrium in the horizontal direction,
f = T = µ(mg – QE), putting this value in (i) we get,
F = T + f = 2f = 2µ(mg – QE)





Post a Comment for "Solutions to Exercises on Friction HC Verma's Concepts of Physics Part 1 (22-26)"