Q#33
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find (a) the maximum height reached and(b) the range of the ball. Take g=10 m/s².Answer:
Given V = 40 m/s, θ = 60° So horizontal component of the velocity
Vx = V cosθ = 40cos 60° = 20 m/s
This component of the velocity will remain unchanged during the flight because there is no acceleration in the horizontal direction.
(a) Vertical component of the velocity Vy = V sin θ = 40 sin 60° = 20√3 m/s.
As we have seen in previous problems that maximum height is given by h = u²/2g
So, we get
h = (20√3)²/20 = 60 m
(b) Range of the ball = (u² sin 2θ)/g, Here u = V = 40 m/s,
So, range x = 40² sin 120° /10 = (1600/10)(√3/2) m = 80√3 m
Q#34
In a soccer practice session, the football is kept at the center of the field 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goalpost?
Answer:
u = 64 ft/s, θ = 45°, Horizontal distance of goalpost =40yards =120 ft,
Range = (u² sin 2θ)/ g
= 64² sin 90°/32 = 128 ft, So the football will touch the ground beyond the goalpost. We need to know the height of the ball when it is vertically in line with the goalpost.
Horizontal velocity = u cos 45° = 64/√2 ft/s
Time taken by the ball to cover the distance of 40 yards
= 120 ft up to the goalpost = 120 ÷ (64/√2) = 15√2/8 s
Now calculate the height of the ball after this time. Vertical component of the velocity
= u sin 45° = 64/√2 ft/s
from h = ut – ½gt²
h = (64/√2)(15√2/8) – ½(32)(15√2/8)²
= 120 – 16(450/64) = 7.5 ft,
Since the height of the goalpost is 10 ft, So, Yes, the football will enter the goalpost.
Q#35
A popular game in Indian villages is Goli which is played with small glass balls called Golis. The Goli of one player is situated at a distance of 2.0 m from the Goli of the second player. This second player has to project his Goli by keeping the thumb of the left hand at the place of his Goli, holding the Goli between his two middle fingers and making the throw. If the projected Goli hits the Goli of the first player, the second player wins. If the height from which Goli is projected is 19.6 cm from the ground and the Goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationary Goli without falling on the ground earlier?
Answer:
Let the required velocity be u. The vertical downward component of the velocity will be zero. If it hits the ground in t seconds to drop vertically a height= 19.6 cm =0.196 m. From the equation
h = ut + ½gt² we get,
0.196 = ½(9.8)t²
t = √(0.196/4.9) = 0.2 s
Now it will hit the ground at a distance = ut = u(0.2) = 0.2u meter
To hit the Goli this distance should be = 2 m, Equating we get,
0.2u = 2
u = 10 m/s.
Q#36
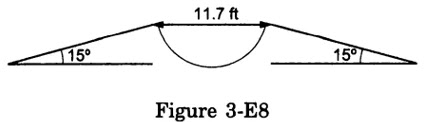
Figure (3-E8) shows an 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch? Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
Answer:
To safely cross the ditch the motorbike should have a minimum range
= 11.7 ft + 5 ft = 16.7 ft
Let the speed of the motorbike for this range be u. θ = 15°,
Range x = (u² sin 2θ )/g
16.7 = (u² sin 30°)/32
u² = 16.7(32)(2)
u = √1068.8 = 32.7 ft/s, is the minimum speed required to cross the ditch.
Q#37
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
Answer:
Let us draw a diagram to understand the problem easily.
Now tan θ = 171/228 = 3/4,
This gives sin θ = 3/5 and cos θ =4/5.
Vertical component of the velocity =u sin θ = 15(3/5) = 9 ft/s
This is the initial velocity of packet for vertical accelerated motion. If the time to reach the ground be t. Using the equation h = ut + ½gt², we get,
171 = 9t + ½(32)t²
16t² + 9t – 171 = 0
t = {-9 ± √(9² + 4(16)(171)}/32
taking only + ve sign for t, we get, t = (-9 + 105)/32 = 3 s.
In this time the packet will travel with the horizontal component of the velocity uniformly.
Horizontal component of velocity = u cos θ = 15(4/5) =12 ft/s.
So the horizontal distance BD = 12 ft/s x 3 s = 36 ft.
So, the packet falls a distance CD ft short of C. CD = BC – BD = 228 – 36 = 192 ft.

Post a Comment for "Solutions to Exercises on Kinematics - Rest And Motion HC Verma's Concepts of Physics Part 1 (33-37)"