Q#38
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?Answer:
We have u = 15 m/s and θ = 60°
So range x = (u² sin 2θ )/g = (225)(√3/2)/9.8 = 19.9 m,
So, Yes, the ball will hit the wall at the distance of 5 m without hitting the floor.
Yes, the answer will differ because the ball will not hit the wall at a distance of 22 m away without hitting the floor.
Q#39
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
Answer:
Between the instants, the projectile crosses half the maximum height its displacement is horizontal, so the direction of average velocity will be horizontal. In the horizontal direction, the projectile has no acceleration so it moves with a uniform velocity equal to u cosθ horizontally.
So, the magnitude of average velocity between the instants the projectile crosses half the maximum height remains u cosθ.
Q#40
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
Answer:
When the plane flying horizontally with a uniform speed, say u, drops a bomb, it gives a uniform horizontal speed u also to the bomb.
So, the bomb will move horizontally just below the plane but their vertical separation will increase with the time. If it explodes in the air, the bomb will be vertically below the plane. See the diagram below.
If the plane flies with an angle θ with the horizontal with uniform speed u, both the plane and the bomb will have same speed and direction at the time of dropping the bomb. Both the plane and the bomb will have a horizontal component of speed equal to 'u cosθ' and vertical component of speed equal to 'u sinθ' at the time of separation. The vertical component of speed 'u sinθ' for the plane remains constant but for the bomb varies according to uniform accelerated motion under the gravity.
So, their vertical separation varies with time. But the horizontal component of the speed 'u cosθ' remains the same, so both the plane and the bomb move with same speed horizontally and even in this case the bomb will explode vertically below the plane. Hence the statement is still true. See the diagram below.
So, their vertical separation varies with time. But the horizontal component of the speed 'u cosθ' remains the same, so both the plane and the bomb move with same speed horizontally and even in this case the bomb will explode vertically below the plane. Hence the statement is still true. See the diagram below.
Q#41
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s² and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
Answer:
First of all we should know the time duration for which the ball is in the air. Let this time be t, vertical displacement in this time is zero. and given that u = 9.8 m/s. From the equation
h = ut – ½gt²
We get,
0 = 9.8t – ½(9.8)t²
½t² – t = 0,
t(t – 2) = 0
t = 0 or 2 s. t = 0 corresponds to the time when it is being projected.
So, the time duration for which it remains in air = 2 s.
Since the ball is projected straight upwards its horizontal velocity with respect to the frame of a railroad car is zero at the instant of projection. But the frame is itself moving with an acceleration of 1 m/s² in the horizontal direction so with respect to this accelerating frame the ball will have equal but backward acceleration during the flight. So, to calculate the horizontal displacement with respect to railroad car we have the following data,
u = 0, a = -1 m/s², t = 2 s, So displacement x = ut + ½at²
= 0 – ½(2)² = -2 m.
Negative sign shows backward displacement. So, the ball will fall 2 m behind the boy on the car.
Q#42
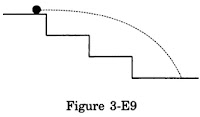
A staircase contains three steps each 10 cm high and 20 cm wide (figure 3-E9). What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane?
Answer:
To hit directly the lowest plane the ball will have to clear point B. From A to B the ball will move a horizontal distance equal to 40 cm = 0.4 m and the vertical distance equal to 20 cm =0.2 m. Let t be the time taken to reach the point be. In this time vertical movement under the gravity has following data,
u = 0, h = 0.2 m, from the equation h = ut + ½gt², we get,
0.2 = 0 + ½(9.8)t²
t² = 0.4/9.8 = 0.04
t = 0.2 s
Let v be the horizontal velocity of the ball, then the horizontal distance traveled by the ball = 0.2 v. In order to clear point B, this must be at least = 0.4,
0.2 v= 0.4
v = 2 m/s.
So, minimum velocity required to hit the lowest floor is 2 m/s.
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s² and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
Answer:
First of all we should know the time duration for which the ball is in the air. Let this time be t, vertical displacement in this time is zero. and given that u = 9.8 m/s. From the equation
h = ut – ½gt²
We get,
0 = 9.8t – ½(9.8)t²
½t² – t = 0,
t(t – 2) = 0
t = 0 or 2 s. t = 0 corresponds to the time when it is being projected.
So, the time duration for which it remains in air = 2 s.
Since the ball is projected straight upwards its horizontal velocity with respect to the frame of a railroad car is zero at the instant of projection. But the frame is itself moving with an acceleration of 1 m/s² in the horizontal direction so with respect to this accelerating frame the ball will have equal but backward acceleration during the flight. So, to calculate the horizontal displacement with respect to railroad car we have the following data,
u = 0, a = -1 m/s², t = 2 s, So displacement x = ut + ½at²
= 0 – ½(2)² = -2 m.
Negative sign shows backward displacement. So, the ball will fall 2 m behind the boy on the car.
Q#42
A staircase contains three steps each 10 cm high and 20 cm wide (figure 3-E9). What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane?
Answer:
To hit directly the lowest plane the ball will have to clear point B. From A to B the ball will move a horizontal distance equal to 40 cm = 0.4 m and the vertical distance equal to 20 cm =0.2 m. Let t be the time taken to reach the point be. In this time vertical movement under the gravity has following data,
u = 0, h = 0.2 m, from the equation h = ut + ½gt², we get,
0.2 = 0 + ½(9.8)t²
t² = 0.4/9.8 = 0.04
t = 0.2 s
Let v be the horizontal velocity of the ball, then the horizontal distance traveled by the ball = 0.2 v. In order to clear point B, this must be at least = 0.4,
0.2 v= 0.4
v = 2 m/s.
So, minimum velocity required to hit the lowest floor is 2 m/s.


Post a Comment for "Solutions to Exercises on Kinematics - Rest And Motion HC Verma's Concepts of Physics Part 1 (38-42)"