Solutions to Exercises on Kinematics - Rest And Motion HC Verma's Concepts of Physics Part 1 (48-52)

 Q#48

Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.

Answer:
Time taken to cross the river = 10/sin θ min.
Net speed of the man in the direction of flow = speed of water + component of man's speed along flow,   

= 5 km/h + 3cos θ km/h 

= (5 + 3cos θ) km/h = 1000(5 + 3cos θ)/60 m/min

So the distance from the point directly opposite the starting point to the point he reaches opposite bank = speed x time

y = 1000(5 + 3cos θ)/60  m/min x 10/sin θ  min  

= (1000/6)(5 + 3cos θ )/sin θ  m =  (1000/6)(5cosecθ + 3cot θ) m

For this to be minimum dy/dθ  = 0 

(1000/6)(-5 cosecθ cotθ - 3cosec²θ) = 0

 cosec θ (5cotθ + 3cosecθ) = 0

either cosecθ = 0 or 5cotθ + 3cosecθ = 0

since cosecθ ≠ 0 we have 5cotθ + 3cosecθ = 0

3 + 5cos θ = 0 

cos θ = -3/5 

sin θ = 4/5

Putting these value in

y = (1000/6)(5cosecθ + 3cot θ) m

y= (1000/6)(25/4 – 9/4) = 4000/6 m = 2/3 km

Q#49
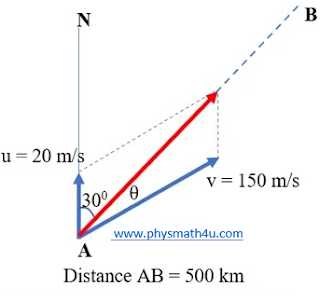
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The airspeed of the plane is 150 m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.

Answer:
Speed of wind u = 20 m/s

Speed of aeroplane v = 150 m/s

(a) To reach point B the pilot should head the plane in such a direction that the resultant velocity is along AB. Let us suppose that the plane heads θ° east of line AB as shown in figure. So, angle between two velocities = θ°+ 30°,

So tan θ° = u sin(θ°+ 30°)/{v + u cos(θ°+ 30°)}

sinθ° {v + u cos(θ° + 30°)} = u cosθ° sin(θ°+ 30°)

sinθ°{v + ucosθ°cos30° - usinθ°sin30°)} = ucosθ°sinθ°cos30° + ucosθ° cosθ°sin30°

vsinθ + (√3/2)usinθ°cosθ°(u/2)sin²θ° = (√3/2)usinθ°cosθ°+ (u/2)cos²θ

vsinθ°- (u/2)sin²θ°= (u/2)cos²θ

v sinθ° = (u/2)(sin²θ°+ cos²θ ) 

v sinθ° = u/2

sinθ° = u/2v = 20/300 = 1/15

θ° = sin^-1(1/15)

So in order to reach point B the plane should head with an angle sin^-1(1/15) east of line AB. 
(b) Angle between u and v = α = 30°+ θ°

Now the resultant velocity

V² = u² + v² + 2uv cos(30 + θ)   

= 20² + 150² + 2.20.150{cos 30°cosθ – sin30°sinθ }

= 400 + 22500 + 6000{(√3/2)√224/15 – (1/2)(1/15)} 
                                
                         {cos θ = √(1 – sin²θ)} = √224/15  

 = 22900 + 6000(√672 – 1)/30 = 27884.6

V = 167 m/s

Distance AB = 500 km = 500,000 m 

Time taken by the plane to reach B = 500,000/167 s

= 500,000/(60 x 167) min = 50 min

Q#50
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beats a drum and B hears the sound t₁time after he sees the event. A and B interchange their position and the experiment is repeated. This time B hears the drum t₂time after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in traveling between the friends.

Answer:
In the first case resultant velocity = u + v 

So, the time taken t₁ = x/(u + v) 

u + v = x/t₁                                                                   (A)

In the second case resultant velocity = v – u 

Now the time taken = t₂ = x/(v – u) 

v – u = x/t₂                                                                   (B) 

Adding the equations (A) and (B) 

2v = x/t₁ + x/t₂

v = (x/2)(1/t₁ + 1/t₂)   It is the velocity of sound in still air.

 Subtracting (B) and (A) we get

2u = x/t₁ - x/t₂

u = (x/2)(1/t₁ – 1/t₂)  It is the velocity of wind.     

Q#51
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of the wind while maintaining the separation x. What will be the time lag B finds between seeing and hearing the drum beating by A?

Answer:

As seen in the above diagram the resultant velocity of sound will be along AB and its magnitude AE can be calculated from the right-angled triangle ACE. 

AE² = AC² - CE² = v² - u² 

AE = √(v² - u²) 

So the time lag B finds between seeing and hearing the drum beating by A

= Distance AB /velocity AE

= x/√(v² - u²) 

Q#52
Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particle will take to meet each other.   

Answer:
Let us draw a diagram.

Consider any particle say A which moves towards B with a speed of v. But the particle B is itself moving with a speed v along BC. So, movement of particle B along the AB direction will be
v.cos∠CBG = vcos60° = v/2. 

Now the relative speed of Particle A with respect to particle B

= v – v/2 = v/2,   

This is the effective speed with which they come closer. To travel a distance of 'a' the time taken
= Distance/speed

= a/(v/2) = 2a/v.

Share :