Q#7
Answer:
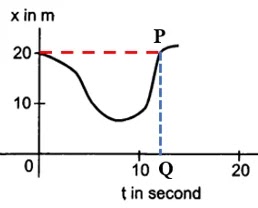
Average velocity in t second will be zero if the displacement at time t will remain equal to the displacement at t = 0 which is 20 m. So, we draw a line parallel to the time axis from 20 m on displacement axis to meet the curve at P (See the figure below). From P draw a line perpendicular to time axis PQ. The time at Q gives the instant when the displacement is again 20 m and average velocity zero. From eye estimation, t = 12 s at Q.
The acceleration of a cart started at t = 0, varies with time as shown in figure (3-E2), Find the distance traveled in 30 seconds and draw the position-time graph.
Answer:
It is clear from the graph that the cart has a uniform acceleration of 5 ft/s² for initial 10 s then uniform velocity for next 10 s (because acceleration is zero) and then retardation in further next 10 s. The area between graph and time axis gives the change in velocity in the taken time interval Let us consider three parts of each 10 s.
In the first 10 s change of velocity = 5 ft/s² x 10 s = 50 ft/s, Since the cart starts from rest at t = 0, average velocity in this period = (50 + 0)/2 = 25 ft/s, Distance travelled in this 10 s = 25 ft/s x 10 s = 250 ft.
From t = 10 s to 20 s area under the graph is zero, so change in velocity is zero, it means that the velocity at t = 10 s (50 ft/s) remains unchanged.
So, distance travelled in this period = 50 ft/s x 10 s = 500 ft.
From t = 20 s to 30 s area under the graph = 5 ft/s² x 10 s = 50 ft/s but it is below the time axis, So this change of velocity is negative. It means that the cart moving with a velocity of 50 ft/s at t = 20 s comes to rest at t = 30 s. So average velocity in this period = 25 ft/s and distance travelled = 25 ft/s x 10 s = 250 ft.
So, the distance travelled = 250 ft + 500 ft+ 250 ft = 1000 ft.
The position-time graph may be drawn as follows,
It is clear from the graph that the cart has a uniform acceleration of 5 ft/s² for initial 10 s then uniform velocity for next 10 s (because acceleration is zero) and then retardation in further next 10 s. The area between graph and time axis gives the change in velocity in the taken time interval Let us consider three parts of each 10 s.
In the first 10 s change of velocity = 5 ft/s² x 10 s = 50 ft/s, Since the cart starts from rest at t = 0, average velocity in this period = (50 + 0)/2 = 25 ft/s, Distance travelled in this 10 s = 25 ft/s x 10 s = 250 ft.
From t = 10 s to 20 s area under the graph is zero, so change in velocity is zero, it means that the velocity at t = 10 s (50 ft/s) remains unchanged.
So, distance travelled in this period = 50 ft/s x 10 s = 500 ft.
From t = 20 s to 30 s area under the graph = 5 ft/s² x 10 s = 50 ft/s but it is below the time axis, So this change of velocity is negative. It means that the cart moving with a velocity of 50 ft/s at t = 20 s comes to rest at t = 30 s. So average velocity in this period = 25 ft/s and distance travelled = 25 ft/s x 10 s = 250 ft.
So, the distance travelled = 250 ft + 500 ft+ 250 ft = 1000 ft.
The position-time graph may be drawn as follows,
Q#8
Figure (3-E3) shows the graph of velocity versus time for a particle going along the X-axis. Find (a) the acceleration, (b) the distance traveled in 0 to 10 s and (c) the displacement in 0 to 10 s.
Answer:
Velocity at t = 0 s is 2 m/s, velocity at t = 10 s is 8 m/s
(a) Acceleration= Change in velocity/time interval = (8 – 2)/10 = 0.6 m/s²
(b) Distance travelled is given by the area under the graph between t = 0 and t = 10 s
= ½(2 + 8) x 10 = 50 m
(c) Since the particle moves in one direction, the magnitude of displacement will be equal to distance travelled = 50 m, along X-axis.
Q#9
Figure (3-E4) shows the graph of the x-coordinate of a particle going along the X-axis as a function of time. Find (a) the average velocity during 0 to 10 s, (b) instantaneous velocity at 2, 5, 8 and 12 s.
Answer:
(a) Displacement during 0 to 10 s = x = 100 m,
Average velocity during 0 to 10 s = 100 m/ 10 s = 10 m/s
(b) Instantaneous velocity at n second, vn is given by the slope of the graph at that instant
v2 = slope of st line at 2 s = 50/2.5 = 20 m/s
v5 = slope of st line at 5 s = zero
v8 = slope of st line at 8 s = (100 – 50)/(10 – 7.5) =50/2.5 = 20 m/s
v12 = slope of st line at 12 s = –100/5 = – 20 m/s (because slope is negative)
Q#10
From the velocity-time plot shown in figure (3-E5), Find the distance traveled by the particle during the first 40 seconds. Also, find the average velocity during the period.
Answer:
Distance traveled by the particle is given by the area between graph and X-axis, the area above X-axis is the distance traveled in the positive direction while the area below X-axis is the distance traveled in the negative direction.
Distance in positive direction = area between t = 0 s to t = 20 s.
= ½ x 20 x 5 = 50 m
Distance in negative direction = area between t = 20 s to t = 40 s.
= ½ x 20 x 5 = 50 m, So total distance travelled = 50 m+ 50 m = 100 m.
Since distance traveled in the positive and negative direction is equal, means the particle returns back to its original position, so displacement is zero
Hence average velocity is zero.
Q#11
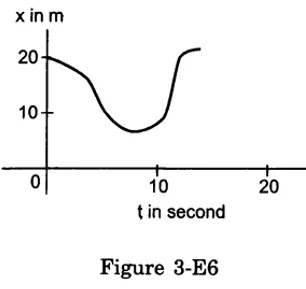
Figure (3-E6) shows x - t graph of a particle. Find the time t such that the average velocity of the particle during the period 0 to t is zero.
Figure (3-E3) shows the graph of velocity versus time for a particle going along the X-axis. Find (a) the acceleration, (b) the distance traveled in 0 to 10 s and (c) the displacement in 0 to 10 s.
Answer:
Velocity at t = 0 s is 2 m/s, velocity at t = 10 s is 8 m/s
(a) Acceleration= Change in velocity/time interval = (8 – 2)/10 = 0.6 m/s²
(b) Distance travelled is given by the area under the graph between t = 0 and t = 10 s
= ½(2 + 8) x 10 = 50 m
(c) Since the particle moves in one direction, the magnitude of displacement will be equal to distance travelled = 50 m, along X-axis.
Q#9
Figure (3-E4) shows the graph of the x-coordinate of a particle going along the X-axis as a function of time. Find (a) the average velocity during 0 to 10 s, (b) instantaneous velocity at 2, 5, 8 and 12 s.
Answer:
(a) Displacement during 0 to 10 s = x = 100 m,
Average velocity during 0 to 10 s = 100 m/ 10 s = 10 m/s
(b) Instantaneous velocity at n second, vn is given by the slope of the graph at that instant
v2 = slope of st line at 2 s = 50/2.5 = 20 m/s
v5 = slope of st line at 5 s = zero
v8 = slope of st line at 8 s = (100 – 50)/(10 – 7.5) =50/2.5 = 20 m/s
v12 = slope of st line at 12 s = –100/5 = – 20 m/s (because slope is negative)
Q#10
From the velocity-time plot shown in figure (3-E5), Find the distance traveled by the particle during the first 40 seconds. Also, find the average velocity during the period.
Answer:
Distance traveled by the particle is given by the area between graph and X-axis, the area above X-axis is the distance traveled in the positive direction while the area below X-axis is the distance traveled in the negative direction.
Distance in positive direction = area between t = 0 s to t = 20 s.
= ½ x 20 x 5 = 50 m
Distance in negative direction = area between t = 20 s to t = 40 s.
= ½ x 20 x 5 = 50 m, So total distance travelled = 50 m+ 50 m = 100 m.
Since distance traveled in the positive and negative direction is equal, means the particle returns back to its original position, so displacement is zero
Hence average velocity is zero.
Q#11
Figure (3-E6) shows x - t graph of a particle. Find the time t such that the average velocity of the particle during the period 0 to t is zero.
Answer:
Average velocity in t second will be zero if the displacement at time t will remain equal to the displacement at t = 0 which is 20 m. So, we draw a line parallel to the time axis from 20 m on displacement axis to meet the curve at P (See the figure below). From P draw a line perpendicular to time axis PQ. The time at Q gives the instant when the displacement is again 20 m and average velocity zero. From eye estimation, t = 12 s at Q.





Post a Comment for "Solutions to Exercises on Kinematics - Rest And Motion HC Verma's Concepts of Physics Part 1 (7-11)"