Solutions to Exercises on Rotational Mechanics HC Verma's Concepts of Physics Part 1 (Q78-Q81)

 Q#78

Figure (10-E14) shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part. 

Answer: 

 For the ball to make a complete circle its weight must balance the centrifugal force at the top of the cylindrical part.
Let the set speed of the ball be v. The angular speed ⍵ = v/r.
The K. E. of the ball

= ½mv² + ½I⍵²
= ½mv²  +½(2mr²/5)(v²/r²)
= ½mv² + mv²/5
= 7mv²/10

Let the speed of the ball at the top position in the cylindrical part be v'.
Similarly, K.E. of the ball at this position = 7mv'²/10
The ball gains P.E. and loses K.E. to the same extent.

7mv²/10 – 7mv'²/10 = (mg)2(R – r)
v² – v'² = 20g(R – r)/7
v'² = v² – 20g(R – r)/7
For the required condition,

mv'²/(R – r) = mg
v'² = g(R – r)
v² – 20g(R – r)/7 = g(R – r)
v² = g(R – r) + 20g(R – r)/7 = 27g(R – r)/7
v = √{27g(R – r)/7}

Q#79
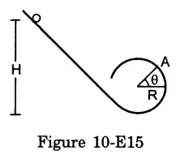
Figure (10-E15) shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and tangential accelerations of the center when the ball is at A.
(c) Find the normal force and the frictional force acting on the ball if H = 60 cm, R = 10 cm, θ = 0 and  m = 70 g.

Answer:
Since the ball is small it means r<<R {Where r is the radius of the ball}. And we shall assume that the ball moves in a circular path of radius R in the loop.

(a) We shall take the lowest point of the track as a reference level for the P.E. The P.E. of the ball at the release = mgH.
The P.E. of the ball at A = mg(R + Rsinθ)
The K.E. of the ball at A = The loss of the P.E.
= mgH – mg(R + Rsinθ)
=mg(H – R – R sinθ)

(b)  Suppose the center of the ball has a linear velocity v at point A, since the ball rolls its angular speed ⍵ = v/r. The K.E. of the ball in terms of v = ½mv²+ ½I⍵²
= ½mv² + ½(2mr²/5)(v²/r²) = ½mv² + mv²/5
= 7mv²/10

Equating it with the K.E. expression in (a)
7mv²/10 = mg(H – R – Rsinθ)
v² = 10g(H – R – Rsinθ)/7                                           (i)

Hence the radial acceleration = v²/R
= 10g(H – R – R sinθ)/7R
= 10g(H/R – 1 – sinθ)/7

The tangential acceleration a = dv/dt
Differentiating (i) w.r.t. t

2vdv/dt = (10g/7){0 – 0 – Rcosθdθ/dt}
2va = –10g⍵Rcosθ/7
a = –5g⍵Rcosθ/7⍵R
a = – (5/7)gcosθ

(c) With the given data,
v² = 10g(0.60 – 0.10 – 0.10sin0°)/7
= 5g/7

The normal force at
A = mv²/R – mgsinθ
= (0.070)(5g/7 x0.10) – 0.070gsin0°
= g/2
= 4.9 N

At θ = 0° the ball is moving in upward direction and its tangential acceleration is
a = – (5/7)g.cos0° = –5g/7 {from (b), the -ve sign is for downward direction i.e. retardation}

The direction of the frictional force F will be upwards as the ball moves in clockwise direction and the at the contact it will push the surface downward.

Hence, F – mg = ma = m(–5g/7)
F = m(g – 5g/7)
= 2mg/7
= 2(0.07)(9.8)/7
= 0.196 N Upwards

Q#80
A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?

Answer:
Let the cue hit at a distance h above the center of the shell with a linear momentum MV.
When the shell sets in motion with a linear speed of the center v and angular speed ⍵, then for slip not to occur on the surface we have, v = r⍵

Since the linear momentum will be conserved MV = mv                                              (i)
[m = mass of the shell]
The angular momentum of the system before the strike about the center of the shell = MVh
The angular momentum of the shell about its center after the strike = I⍵

= (2mR²/3)(v/R)
= 2mvR/3
Since there is no external torque the angular momentum is conserved.

MVh = 2mvR/3
mvh = 2mvR/3       {From (i)}
h = 2R/3.

So the shell should be hit 2R/3 above the center.

Q#81

A uniform wheel of radius R is set into rotation about its axis at an angular speed ⍵. This rotating wheel is now placed on a rough horizontal surface with its axis horizontal. Because of friction at the contact, the wheel accelerates forward and its rotation decelerates till the wheel starts pure rolling on the surface. Find the linear speed of the wheel after it starts pure rolling.

Answer:
Let the mass of the wheel = m, the moment of inertia of the wheel about its rotational axis I = ½mR²
Hence its angular momentum P = I⍵ = ½mR²⍵

When the wheel starts pure rolling, the point of contact remains stationary and the wheel rotates about an axis passing through the point of contact and parallel to the original axis (pure rotation). Hence the angular momentum of the wheel about this axis P' = I'⍵'

Let the linear speed of the wheel when it starts pure rolling = v, so its angular speed ⍵' = v/R. And

I' = I + mR² = ½mR² + mR² = 3mR²/2
P' = (3mR²/2)(v/R) = 3mvR/2

Since in the absence of an external torque the angular momentum will be conserved, i.e.

P' = P
3mvR/2 = ½mR²⍵
v = ⍵R/3

Share :