Q#39
A uniform chain of length L and mass M overhangs a horizontal table with its two-third part on the table. The friction coefficient between the table and the chain is µ. Find the work done by the friction during the period the chain slips off the table.Answer:
Weight of the chain on the table = 2Mg/3
Normal force on the chain = Weight of the chain = 2Mg/3
Force of friction on the chain
= µN = 2µMg/3
As the chain slips on the table its weight on the table and hence normal force and friction force starts decreasing. Just when the chain slips off the friction force becomes zero.
Hence average friction force
= F =(2µMg/3)/2 = 2µMg/6
Work done by the friction force = Force x distance
= (2µMg/6) x (-2L/3)
= -2µMgL/9
Q#40
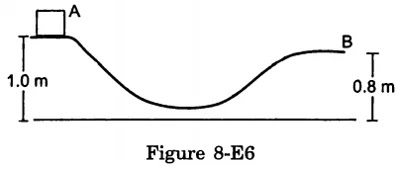
A block of mass 1 kg is placed at a point A of a rough track shown in the figure (8-E6). If slightly pushed towards the right, it stops at point B of the track. Calculate the work done by the frictional force on the block during its transit from A to B.
Answer:
The block descends by 1.0 m - 0.8 m = 0.2 m in coming from A to B. Potential energy lost = mgh =1.0 x 10 x 0.2 J = 2.0 J
If there would not have been the frictional force, this lost P.E. would be converted to K.E. Since at point B the block stops, hence no K.E. at B.
So, in this case, the negative work done by the frictional force is just equal to the P.E. lost i.e. = -2.0 J
Q#41
A block of mass 5.0 kg is suspended from the end of a vertical spring which is stretched by 10 cm under the load of the block. The block is given a sharp impulse from below so that it acquires an upward speed of 2.0 m/s. How high the will it rise? Take g=10 m/s².
Answer:
K.E. given to the block = ½mv²
Let it rise to a height of h,
At the highest point change in P.E. = mgh
At this point total K.E. is converted to P.E.
i.e.
mgh = ½mv²
h = v²/2g = 2 x 2/(2 x 10) m = 1/5 m = 20 cm
Q#42
A block of mass 250 g is on a vertical spring of spring constant 100 N/m fixed from below.The spring is now compressed to have a length 10 cm shorter than its natural length and the system is released from this position. How high does the block rise? Take g=10 m/s².
Answer:
Work done on the spring = ½kx² = ½(100)(0.10)² = 0.50 J
= Potential energy stored in the spring
When the system is released the block rises to a height of, say h. At the highest point P.E. =mgh
It will be equal to P.E. stored in the spring.
So, mgh = 0.50
h = 0.50/(0.25 x 10) m = 0.20 m = 20 cm
Figure (8-E7) shows a spring fixed at the bottom end of an incline of inclination 37°. A small block of mass 2.0 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) the friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s².
Answer:
Let us draw a free body diagram of the block as below,
(a) Forces on the block are weight mg, the force of friction F and normal force on the block N.
Equating the forces perpendicular to the plane,
N = mgcos37°
Resolving all the forces along the plane we get net force
= mgsin37° – µN = mgsin37° – µmgcos37°
Distance covered along the plane = 4.8 m+ 0.20 m = 5.0 m
= (mgsin 37° – µmgcos37°) x 5.0 J (i)
This work done is stored as potential energy in the spring compression = ½kx² (where k=spring constant and x = compression of spring)
= ½k(0.20)² J
When the block rebounds this stored P.E. is utilized in the movement of the block. In the return journey, the magnitude of the friction force remains the same but it's direction changes because it resists the movement. Now forces along the plane are
= mgsin37°+ F = mgsin37°+ µmgcos37°
Now it moves to a distance of 1.0 m
So, work done by the forces = Force x distance
= (mgsin37° + µmgcos37°) x 1.0
= mg sin37° + µmgcos37° J
All (i), (ii) and (iii) are equal. Equating (i) and (iii)
mgsin37° + µmgcos37° = (mgsin37° – µmgcos37°) x 5.0
µ(6mg)cos37° = 4mg(sin37°)
µ = 2tan37°/3 = 2(0.75)/3 = 0.50
(b) Equating (ii) and (iii) we get,
½kx² = mgsin37° + µmgcos37°
k(0.20)² = 2mg(sin37° + µcos37°)
k = 2(2)(10)[0.60 + 0.50(0.80)]/0.04
k = 40(100)1.0/4 = 1000 N/m


Post a Comment for "Solutions to Exercises on Work and Energy HC Verma's Concepts of Physics Part 1 (39-43)"