Solutions to Exercises on Work and Energy HC Verma's Concepts of Physics Part 1 (8-12)

 Q#8

A force a + bx acts on a particle in the x-direction where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.

Answer:
Displacement of the particle = d-0 = d
Force at x = 0, F = a
and at x = d is F' = a +bd

Average force = (F + F')/2

= (a + a + bd)/2
= a + ½bd

Work done = Force x Displacement

W = (a + ½bd)d

Q#9
A block of mass 250 g slides down an incline of inclination 37° with a uniform speed. Find the work done against the friction as the block slides through 1.0 m.

Answer:
Given: Mass m = 250 g = 0.25 kg
Weight = mg = 0.25(10 N) = 2.5 N  (Taking g =10 m/s²)
The force against friction is the component of weight along the incline = mg sin37°
Displacement given = 1.0 m

So, work done = Force x Displacement

W = mgsin37° x 1.0 J
= 2.5 sin37° J
W = 1.50 J

Q#10
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (Figure 8-E1). A constant horizontal force F acting on the lower block produces an acceleration F/2(m + M) in the system, the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.

Answer:
(a) Weight of the system = (m + M)g = N  (N = Normal force)
Force of friction = µN

= µ(m + M)g

Given that acceleration a = F/2(m + M)

Now equation of forces along the surface is

F – µN= (m + M)a
F – µ(m + M)g = (m + M)F/2(m + M) = F/2
2F – 2µg(m + M) = F
2µg(m + M) = F
µ = F/{2g(m + M)}

(b) Let f be the frictional force acting on the smaller block. Along the movement, only this force is on the block which has acceleration = F/2(m + M)

So this force should be equal to mass x acceleration,

= mF/2(m + M)

(c) During a displacement d, velocity of the block will be given as

v² = u² + 2ad = 2ad                              (Since u = 0)
v² = 2Fd/2(m + M) = Fd/(m + M)

Final K.E. = ½mv² = mFd/2(m + M)

Initial K.E. = 0
Change in K.E. = mFd/2(m + M)

So work done by the frictional force on the smaller block by the larger block

= Change in its kinetic energy
= mFd/2(m + M)

Q#11
A box weighing 2000 N is to be slowly slid through 20 m on a straight track having friction coefficient 0.2 with the box, (a) Find the work done by the person pulling the box with a chain at an angle θ with the horizontal. (b) Find the work when the person has chosen a value of θ which ensures him the minimum magnitude of the force. 

Answer:
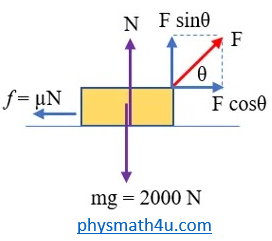
First let us draw a Free body diagram of the box to show the forces acting on it.

If the pull applied by the person is F,

Then Normal force
N + Fsinθ = W = 2000 Newton
N = 2000 – Fsinθ

Force of friction

f = µN = 0.2 x (2000 – F sinθ) = 400 – 0.2 x Fsinθ

Since the box is to be slowly slid, which means the driving force is just equal to frictional force.
This driving force

Fcosθ = 400 – 0.2 x Fsinθ
F(cosθ + 0.2 sinθ) = 400
F(5cosθ + sinθ) = 2000                (Multiply both sides by 5)
F = 2000/(5 cosθ + sinθ)

Since the block is to be slid through a distance of 20 m

(a) So work done by the person

W = Fcosθ x 20 J

= 2000 x cosθ x 20/(5 cosθ + sinθ) J
= 40000/(5 + tanθ) J

(b) For F to be minimum, dF/dθ = 0.

So,
 –2000(–5sinθ + cosθ)/(5cosθ + sinθ)² = 0
cosθ = 5sinθ
tanθ = 1/5

(So F is minimum for that value of θ for which tanθ = 1/5)

Putting this value in the work done expression we get,

W = 40000/(5 + 1/5) = 7692 J

Q#12
A block of weight 100 N is slowly slid up on a smooth incline of inclination 37° by a person. Calculate the work done by the person in moving the block through a distance of 2.0 m, if the driving force is (a) parallel to the incline and (b) in the horizontal direction.   

Answer:
(a) Driving force parallel to the incline
Since the block is slowly slid up, that means driving force parallel to incline is just equal to the resisting force which is a component of weight. See the figure below,

So, driving force F = 100 x sin37° N
Work done,

W = F x d = 100 x sin37° x 2.0 = 120 J

(b) Driving force in the horizontal direction
When the driving force is in the horizontal direction, its component along incline will be equal to the force F = 100 x sin37° N

So even in this case work done = 120 J

Share :