Freely Falling Objects Problems and Solutions 1

Q#41

(II) The best rebounders in basketball have a vertical leap (that is, the vertical movement of a fixed point on their body) of about 120 cm. 

(a) What is their initial “launch” speed off the ground? 

(b) How long are they in the air? 

Answer:

Choose upward to be the positive direction, and take 0y = 0 to be at the floor level, where the jump starts. For the upward path, y = 1.2 m, $v_y$ = 0 at the top of the path, and $a_y$ = −9.80 $m/s^2$.

(a) The initial speed can be found from Eq. 

$v_{y}^2=v_{0y}^2+2a_y(y-y_0)$, 

with x replaced by y. 

$v_{0y}=\sqrt{v_y^2-2a_y(y-y_0)}$

$v_{0y}=\sqrt{0^2-2(-9.80 \ m/s^2)(1.20 \ m-0)}=4.85 \ m/s$

(b) The time of flight can be found from Eq. 

$y-y_0=v_{0y}t+\frac{1}{2}a_yt^2$

with x replaced by y, using a displacement of 0 for the displacement of the jumper returning to the original height. 

$0=0+v_{0y}t+\frac{1}{2}at^2$

$0=t(v_{0y}t+\frac{1}{2}at)$ so

t = 0 or $t=\frac{2v_{0y}}{a}=\frac{2(4.897 \ m/s)}{-(-9.80 / m/s^2)}=0.99 \ s$

The result of t = 0 s is the time for the original displacement of zero (when the jumper started to jump), and the result of t = 0.99 s is the time to return to the original displacement. 

Thus the answer is t = 0.99 seconds. 

Q#42

(II) An object starts from rest and falls under the influence of gravity. Draw graphs of 

(a) its speed and 

(b) the distance it has fallen, as a function of time from t = 0 to t = 5.00 s. Ignore air resistance. 

Answer:

Choose downward to be the positive direction, and take $y_0$ = 0 to be at the height where the object was released. 

The initial velocity is $v_y$ = 0, and the acceleration is a = 9.80 $m/s^2$.

(a) The speed of the object will be given by 

$v_y=v_{0y}+a_yt$

with $v_y$ = 0, so 

$v_y$ = at = (9.80 $m/s^2$)t.

This is the equation of a straight line passing through the origin with a slope of 9.80 $m/s^2$.

(b) The distance fallen will be given by Eq. 

$y-y_0=v_{0y}t+\frac{1}{2}a_yt^2$

with $v_y$ = 0, so 

$y-0=0+\frac{1}{2}(4.90 \ m/s^2)t^2$

This is the equation of a parabola, with its vertex at the origin, opening upward.

Q#43

(II) A stone is thrown vertically upward with a speed of 24.0 m/s.

(a) How fast is it moving when it is at a height of 13.0 m? 

(b) How much time is required to reach this height? 

(c) Why are there two answers to (b)? 

Answer:

Choose upward to be the positive direction, and $y_0$ = 0 to be the height from which the stone is thrown. 

We have $v_{0y}$ = 24.0 m/s, a = −9.80 $m/s^2$, and $y-y_0$ = 13.0 m.

(a) The velocity can be found from Eq. 

$v_{y}^2=v_{0y}^2+2a_y(y-y_0)$, 

with x replaced by y. 

$v_{y}=\pm \sqrt{v_{0y}^2+2a_y(y-y_0)}$

$v_{y}=\pm \sqrt{(24.0 \ m/s^2)^2+2(-9.80 \ m/s^2)(13.0 \ m-0)}$

$v_y=\pm 17.9 \ m/s$

Thus, $|v_y|=17.9 \ m/s$ 

(b) The time to reach that height can be found from Eq. 

 $y-y_0=v_{0y}t+\frac{1}{2}a_yt^2$

$13.0 \ m=(24.0 \ m/s)t+\frac{1}{2}(-9.80 \ m/s^2)t^2$

$0=\frac{2 \times -13.0 \ m}{-9.80 \ m/s^2}+\frac{(2 \times 24.0 \ m/s)}{-9.80 \ m/s^2}t+\frac{1}{2}t^2$

$t^2-4.898t+2.653=0$

$t_{12}=\frac{4.898 \pm \sqrt{(4.898)^2-4(1)(2.653)}}{2(1)}$

$t_{12}=\frac{4.898 \pm \sqrt{13.3784}}{2}$

$t_{1}=\frac{4.898 +\sqrt{13.3784}}{2}$ or $t_{2}=\frac{4.898 - \sqrt{13.3784}}{2}$

we get $t_1=4.28 \ s$ or $t_2=0.620 \ s$

(c) There are two times at which the object reaches that height—once on the way up (t = 0.620 s) and once on the way down (t = 4.28 s).

Q#44

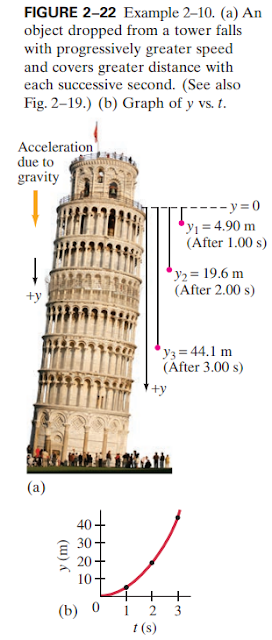
(II) For an object falling freely from rest, show that the distance traveled during each successive second increases in the ratio of successive odd integers (1, 3, 5, etc.). (This was first shown by Galileo.) See Figs. 2–19 and 2–22. 

Answer:

Choose downward to be the positive direction, and take $y_0$ = 0 to be the height from which the object is released. The initial velocity is $v_y$ = 0, and the acceleration is a = g. 

Then we can calculate the position as a function of time from Eq. 

 $y-y_0=v_{0y}t+\frac{1}{2}a_yt^2$

with x replaced by y, as $y(t)=\frac{1}{2}gt^2$.

At the end of each second, the position would be as follows: 

y(0) = 0; $y(1)=\frac{1}{2}g$; 

$y(2)=\frac{1}{2}g(2)^2=4y(1)$

$y(3)=\frac{1}{2}g(3)^2=9y(1)$

The distance traveled during each second can be found by subtracting two adjacent position values from the above list.

d(1) = y(1) - y(0) = y(1)

d(2) = y(2) - y(1) = 3y(1)

d(3) = y(3) - y(2) = 5y(1)

We could do this in general. Let n be a positive integer, starting with 0.

$y(n)=\frac{1}{2}gn^2$ 

$y(n + 1)=\frac{1}{2}g(n+1)^2$ 

d(n + 1) = y(n+1) - y(n)

d(n + 1) = $\frac{1}{2}g(n+1)^2-\frac{1}{2}gn^2$

 = $\frac{1}{2}g((n+1)^2-n^2)$

 = $\frac{1}{2}g(n^2+2n+1-n^2)$

 = $\frac{1}{2}g(2n+1)$

The value of (2n + 1) is always odd, in the sequence 1, 3, 5, 7, .

Q#45

(II) A rocket rises vertically, from rest, with an acceleration of 3.20 $m/s^2$ until it runs out of fuel at an altitude of 775 m. After this point, its acceleration is that of gravity, downward. 

(a) What is the velocity of the rocket when it runs out of fuel? 

(b) How long does it take to reach this point? 

(c) What maximum altitude does the rocket reach? 

(d) How much time (total) does it take to reach maximum altitude? 

(e) With what velocity does it strike the Earth? 

(f) How long (total) is it in the air?

Answer:

(a) Choose upward to be the positive direction, and $y_0$ = 0 at the ground. The rocket has $v_{0y}$ = 0, a = 3.2 $m/s^2$ , and y = 775 m when it runs out of fuel. 

Find the velocity of the rocket when it runs out of fuel from Eq. 

$v_{y}^2=v_{0y}^2+2a_y(y-y_0)$,             (*)

with x replaced by y. 

$v_{775m}^2=v_{0y}^2+2a_y(y-y_0)$, 

$v_{775m}=\pm\sqrt{v_{0y}^2+2a_y(y-y_0)}$

$v_{775m}=\pm\sqrt{0+2(3.20 \ m/s^2)(775 \ m)}$

$v_{775m}=70.43 \ m/s$

The positive root is chosen since the rocket is moving upward when it runs out of fuel.

(b) The time to reach the 775 m location can be found from Eq. 

$v_y=v_(0y)+a_yt$

$t_{775m}=\frac{v_{775m}-v_{0y}}{a_y}$

$t_{775m}=\frac{70.43 \ m/s-0}{3.2 \ m/s^2}=22.01 \ s$

(c) For this part of the problem, the rocket will have an initial velocity $v_{0y}$ = 70.43 m/s, an acceleration of a = −9.80 $m/s^2$, and a final velocity of $v_y$ = 0 at its maximum altitude. 

The altitude reached from the out-of-fuel point can be found from Eq. (*)

$v_{775m}^2=v_{0y}^2+2a_y(y-775 \ m)$

$y_{max}=775 \ m + \frac{0-(-70.43 \ m/s)^2}{2(-9.80 \ m/s^2)}$

$y_{max}=775 \ m + 253 \ m=1028 \ m$

(d) The time for the “coasting” portion of the flight can be found from Eq. 

$v_y=v_{0y}+a_yt$

$v_y=v_{775m}+a_yt_{coast}$

$t_{coast}=\frac{0-70.43 \ m/s}{-9.80 \ m/s^2}=7.90 \ s$

Thus the total time to reach the maximum altitude is 

t = 22.01 s + 7.90 s = 29.20 s

(e) For this part of the problem, the rocket has $v_{0y}$ = 0 m/s, a = −9.80 $m/s^2$, and a displacement of −1028 m (it falls from a height of 1028 m to the ground). 

Find the velocity upon reaching the Earth from Eq. 

$v_{y}=\pm \sqrt{v_{0y}^2+2a_y(y-y_0)}$

$v_{y}=\pm \sqrt{0^2+2(-9.80 \ m/s^2)(-1028 \ m)}$

$v_y=-141.95 \ m/s$

The negative root was chosen because the rocket is moving downward, which is the negative direction.

(f) The time for the rocket to fall back to the Earth is found from Eq.

$v_y=v_{0y}+a_yt$

$t_{fall}=\frac{v_y-v_{0y}}{a_y}$

$t_{fall}=\frac{-141.95 \ m/s}{-9.80 \ m/s^2}=14.48 \ s$

Thus the total time for the entire flight is t = 29.20 s + 14.48 s = 43.68 s ≈ 44 s.

Share :