Q#56
The acceleration due to gravity on the Moon is about onesixth what it is on Earth. If an object is thrown vertically upward on the Moon, how many times higher will it go than it would on Earth, assuming the same initial velocity?
Answer:
Choose the upward direction to be positive and $y_0$ = 0 to be the level from which the object was thrown. The initial velocity is $v_{0y}$ and the velocity at the top of the path is $v_y$ = 0. The height at the top of the path can be found from Eq.
$v_y^2=v_{0y}^2+2a_y (y-y_0)$ with x replaced by y.
$y-y_0=\frac{-v_{0y}^2}{2a_y}$
From this we see that the displacement is inversely proportional to the acceleration, so if the acceleration is reduced by a factor of 6 by going to the Moon, and the initial velocity is unchanged, then the displacement increases by a factor of 6.
Q#57
A person who is properly restrained by an over-the-shoulder seat belt has a good chance of surviving a car collision if the deceleration does not exceed 30 “g’s”(1.00 g = 9.80 $m/s^2$). Assuming uniform deceleration at 30 g’s, calculate the distance over which the front end of the car must be designed to collapse if a crash brings the car to rest from 95 km/h.
Answer:
We are treating the value of 30 g’s as if it had 2 significant figures. The initial velocity of the car is
$v_0=(95 \ km/h)\left(\frac{1000 \ m/km}{3600 \ s/h}\right)=26.39 \ m/s$
Choose $x_0$= 0 to be location at which the deceleration begins. We have v = 0 and a = -30g = $-294 \ m/s^2$
Find the displacement from Eq.
$v^2=v_{0}^2+2a (x-x_0)$
$x-x_0=\frac{v^2-v_{0}^2}{2a}$
$x-0=\frac{0-(26.39 \ m/s)^2}{2(-294 \ m/s^2)}=1.18 \ m$
Q# 58
A person jumps out a fourth-story window 18.0 m above a firefighter’s safety net. The survivor stretches the net 1.0 m before coming to rest, Fig. 2–45.
(a) What was the average deceleration experienced by the survivor when she was slowed to rest by the net?
(b) What would you do to make it “safer” (that is, to generate a smaller deceleration): would you stiffen or loosen the net? Explain.
Answer:
(a) For the free-falling part of the motion, choose downward to be the positive direction and $y_0$ = 0 to be the height from which the person jumped.
The initial velocity is $v_{0y}$ = 0, acceleration is $a_y$ = 9.80 $m/s^2$, and the location of the net is y = 18.0 m.
Find the speed upon reaching the net from Eq.
$v_y^2=v_{0y}^2+2a_y (y-y_0)$
with x replaced by y.
$v_y=\pm \sqrt{0+2a(y-y_0)}$
$v_y=\pm \sqrt{2(9.80 \ m/s^2)(18.0 \ m)}=18.78 \ m/s$
The positive root is selected since the person is moving downward. For the net-stretching part of the motion, choose downward to be the positive direction, and $y_0$ = 18.0 m to be the height at which the person first contacts the net.
The initial velocity is $v_{0y}$ = 18.78 m/s, the final velocity is $v_y$ = 0, and the location at the stretched position is y = 19.0 m. Find the acceleration from Eq.
$v_y^2=v_{0y}^2+2a_y (y-y_0)$
with x replaced by y.
$a_y=\frac{v_y^2-v_{0y}^2}{2(y-y_0)}$
$a_y=\frac{0-(18.79 \ m/s)^2}{2(1.0 \ m)}=-178 \ m/s^2$
This is about 18 g’s.
(b) For the acceleration to be smaller, in the above equation we see that the displacement would have to be larger. This means that the net should be loosened.
Q#59
A bicyclist in the Tour de France crests a mountain pass as he moves at 15 km/h. At the bottom, 4.0 km farther, his speed is 65km/h. Estimate his average acceleration (in $m/s^2$) while riding down the mountain.
Answer:
The initial velocity is $v_0$= 15 km/h, the final velocity is v = 65 km/h, and the displacement is $x-x_0$= 4.0 km = 4000 m. Find the average acceleration from Eq.
$v^2=v_{0}^2+2a (x-x_0)$
$a=\frac{v^2-v_{0}^2}{2(x-x_0)}$
$a=\frac{(65 \ km/h)^2-(15 \ km/h)^2}{2(4.0 \ km)}=500 \ km/h^2$
$a=(500 \ km/h^2)\left(\frac{1000 \ m/km}{(3600 \ s/h)^2}\right)=0.0385 \ m/s^2$
Q#60
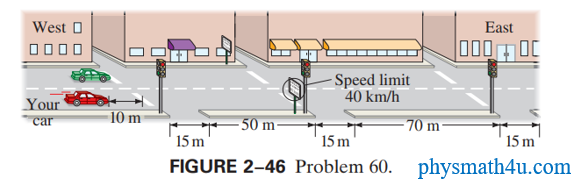
Consider the street pattern shown in Fig. 2–46. Each intersection has a traffic signal, and the speed limit is 40 km/h. Suppose you are driving from the west at the speed limit. When you are 10.0 m from the first intersection, all the lights turn green. The lights are green for 13.0 s each.(a) Calculate the time needed to reach the third stoplight. Can you make it through all three lights without stopping?
(b) Another car was stopped at the first light when all the lights turned green. It can accelerate at the rate of 2.00 $m/s^2$ to the speed limit. Can the second car make it through all three lights without stopping? By how many seconds would it make it, or not make it?
Answer:
The speed limit is $(40 \ km/h)\left(\frac{1000 \ m/km}{3600 \ s/h}\right)=11.11 \ m/s$
(a) For your motion, you would need to travel (10 + 15 + 50 + 15 + 70) m = 160 m to get the front of the car to the third stoplight. The time to travel the 160 m is found using the distance and the speed limit.
$\Delta x = \overline{v}\Delta t$
$\Delta t = \frac{\Delta x}{\overline{v}}=\frac{160 \ m}{11.11 \ m/s}=14.40 \ s$
No , you cannot make it to the third light without stopping, since it takes you longer than 13.0 seconds to reach the third light.
(b) The second car needs to travel 165 m before the third light turns red. This car accelerates from $v_0$ = 0 to a maximum of v = 11.11 m/s with a = 2.00 $m/s^2$. Use Eq. $v=v_0+at$ to determine the duration of that acceleration.
$t_{acc}=\frac{v-v_0}{a}$
$t_{acc}=\frac{11.11 \ m/s-0}{2.00 \ m/s^2}=5.556 \ s$
The distance traveled during that time is found from Eq. $x-x_0=v_0t+\frac{1}{2}at^2$
$(x-x_0)_{acc}=v_0t_{acc}+\frac{1}{2}at_{acc}^2$
$x-x_0=0+\frac{1}{2}(2.00 \ m/s^2)(5.556 \ s)^2=30.87 \ m$
Since 5.556 s have elapsed, there are 13.0 – 5.556 = 7.444 s remaining to clear the intersection.
The car travels another 7.444 s at a speed of 11.11 m/s, covering a distance of
$\Delta x_{constant \ speed}=v_{avg}t$
$\Delta x_{constant \ speed}=(11.11 \ m/s)(7.444 \ s) = 82.70 \ m$
Thus the total distance is 30.87 m + 82.70 m = 113.57 m.
No , the car cannot make it through all three lights without stopping.
The car has to travel another 51.43 m to clear the third intersection and is traveling at a speed of 11.11 m/s. Thus the front of the car would clear the intersection a time
$t = \frac{\Delta x}{v}=\frac{51.43 \ m}{11.11 \ m/s}=4.6 \ s$ after the light turns red.

Post a Comment for " Kinematics in One Dimension Problems and Solutions "