The First Law of Thermodynamics Problems and Solutions 3

Q#19.47

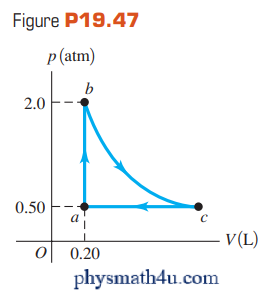
Figure P19.47 shows a pV-diagram for 0.0040 mole of ideal gas. 

The temperature of the gas does not change during segment bc. 

(a) What volume does this gas occupy at point c? 

(b) Find the temperature of the gas at points a, b, and c. 

(c) How much heat went into or out of the gas during segments ab, ca, and bc? Indicate whether the heat has gone into or out of the gas. 

(d) Find the change in the internal energy of this hydrogen during segments ab, bc, and ca. Indicate whether the internal energy increased or decreased during each of these segments. 

Answer:

Segment ab is isochoric, bc is isothermal, and ca is isobaric.

For bc, $\Delta T = 0$, $\Delta U = 0$ and $Q = W = nRT ln \left(\frac{V_c}{V_b}\right)$

For ideal $H_2$ (diatomic), $C_v=\frac{5}{2}R$ and $C_p=\frac{7}{2}R$ 

$\Delta U = nC_v\Delta T$ for any process of an ideal gas.

(a) $T_b=T_c$. For states b and c, pV = nRT = constant so

$p_bV_b=p_cV_c$

$V_c=V_b\left(\frac{p_b}{p_c}\right)$

$V_c=(0.20 \ L)\left(\frac{2.0 \ atm}{0.50 \ atm}\right)=0.80 \ L$

(b) $T_a=\frac{p_aV_a}{nR}$

$T_a=\frac{(0.50 \ atm)(1.013 \times 10^5 \ Pa/atm)(0.20 \times 10^{-3} \ m^3)}{(0.0040 \ mol)(8.3145 \ J/mol.K)}$

$T_a=305 \ K$

For states a and b, $V_a=V_b$, so

$\frac{T}{p}= \frac{nR}{V}$ = constant, so we write

$\frac{T_a}{p_a}=\frac{T_b}{p_b}$

$T_b=T_c=T_a\left(\frac{p_b}{p_a}\right)$

$T_b=(305 \ K)\left(\frac{2.0 \ atm}{0.50 \ atm}\right)=1220 \ K=T_c$

(c) For states a and b, Q = $nC_v\Delta T=n\left(\frac{5}{2}R\right)\Delta T$, which gives

$Q = (0.0040 \ mol)\left(\frac{5}{2}(8.3145 \ J/mol.K)\right)(1220 \ K - 305 \ K)=+76 \ J$

Q is positive and heat goes into the gas.

For states c and a, Q = $nC_p\Delta T=n\left(\frac{7}{2}R\right)\Delta T$, which gives

$Q = (0.0040 \ mol)\left(\frac{7}{2}(8.3145 \ J/mol.K)\right)(305 \ K - 1220 \ K)=-107 \ J$

Q is negative and heat comes out of the gas.

For states b and c:

$Q=W = nRT ln \left(\frac{V_c}{V_b}\right)$, which gives

$Q= (0.0040 \ mol)(8.3145 \ J/mol.K)(1200 \ K) ln \left(\frac{0.80 \ L}{0.20 \ L}\right)=+56 \ J$

Q is positive and heat goes into the gas.

(d)  For states a and b: 

$\Delta U = nC_v\Delta T$ 

$\Delta U=n\left(\frac{5}{2}R\right)\Delta T$, which gives

$\Delta U = (0.0040 \ mol)\left(\frac{5}{2}(8.3145 \ J/mol.K)\right)(1220 \ K - 305 \ K)=+76 \ J$

The internal energy increased. 

For states b and c:

ΔT = 0 so ΔU = 0. The internal energy does not change.

For states c and a: 

$\Delta U = nC_v\Delta T$ 

$\Delta U=n\left(\frac{5}{2}R\right)\Delta T$, which gives

$\Delta U = (0.0040 \ mol)\left(\frac{5}{2}(8.3145 \ J/mol.K)\right)(305 \ K - 1220 \ K)=-76 \ J$

 The internal energy decreased.

The net internal energy change for the complete cycle a → b → c → d is $\Delta U_tot=+76 \ J +0+(-76 \ J)=0$. 

For any complete cycle the final state is the same as the initial state and the net internal energy change is zero. For the cycle the net heat flow is

$\Delta Q_tot=+76 \ J +(-107 \ J)+56 \ J=+25 \ J$. 

The net work done in the cycle is positive and this agrees with our result that the net heat flow is positive.

Share :