Q#12 (Past Exam Paper – November 2017 Paper 22 Q2)
(a) Define the moment of a force. [1]
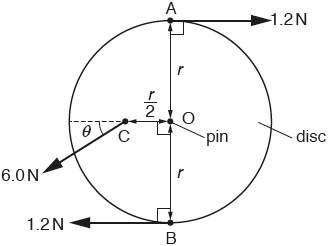
(b) A thin disc of radius r is supported at its centre O by a pin. The disc is supported so that it is vertical. Three forces act in the plane of the disc, as shown in Fig. 2.1.
Fig. 2.1
Two horizontal and opposite forces, each of magnitude 1.2 N, act at points A and B on the edge of the disc. A force of 6.0 N, at an angle θ below the horizontal, acts on the midpoint C of a radial line of the disc, as shown in Fig. 2.1. The disc has negligible weight and is in equilibrium.
(i) State an expression, in terms of r, for the torque of the couple due to the forces at A and B acting on the disc. [1]
(ii) Friction between the disc and the pin is negligible.
Determine the angle θ. [2]
(iii) State the magnitude of the force of the pin on the disc. [1]
[Total: 5]
Solution:
(a) The moment of a force is defined as the product of the force and the perpendicular of the line of action of the force to a point.
(b)
(i)
{Torque = force × perpendicular distance between the 2 forces
Torque = 1.2 × 2r}
Torque = 2.4r
or (1.2 × 2r) or (1.2r + 1.2r)
(ii)
{Since the disc is in equilibrium, anticlockwise moment = clockwise moment
Clockwise moment (due to forces at A and B) = (1.2 × r) + (1.2 × r) = 2.4r
Recall: Moment = force × perpendicular distance
The force at C acts at a distance r/2 from the pin.
Perpendicular component of force = 6.0 sinθ}
Anticlockwise moment = 6.0 × r / 2 × sinθ
{Anticlockwise moment = clockwise moment}
6.0 × r / 2 × sinθ = 2.4r
θ = 53°
(iii)
{For equilibrium,
Resultant torque / moment = 0
(rotational equilibrium,) – this was already seen in the previous parts
Resultant force = 0 (translational equilibrium)
The 1.2 N forces cancel each other. So, we need another 6.0 N force for equilibrium.}
Force = 6.0 N
Post a Comment for "(a) Define the moment of a force. (b) A thin disc of radius r is supported at its centre O by a pin"